Kaspa: The Next Generation Protocol
A Comprehensive Guide to BlockDAG, Consensus, and the Future of Digital Currency
Introduction
Welcome to this comprehensive guide dedicated to Kaspa, a cryptocurrency that doesn't just iterate on existing technologies, but fundamentally reinvents them. In an ecosystem where thousands of projects compete for attention, Kaspa distinguishes itself with a rigorous approach and profound innovations that aim to solve the most fundamental problems of traditional blockchains: scalability, speed, and decentralization, without compromise.
This book aims to demystify the complex concepts underlying Kaspa. We will start with the basics, explaining what a Directed Acyclic Graph (DAG) is and how Kaspa's GHOSTDAG protocol uses it to create a consensus system that is fast, secure, and fully decentralized. Whether you are a curious developer, an investor seeking to understand the underlying technology, or simply a cryptocurrency enthusiast, this book is designed to guide you step by step.
We will explore how Kaspa has solved the "blockchain trilemma," how its unique architecture enables near-instant confirmations, and how it manages data storage sustainably through a sophisticated pruning system. We will also cover more advanced topics such as its resistance to MEV (Maximal Extractable Value), its vision for Layer 2 solutions with ZK-Rollups, and the economic dynamics of its fee market.
This work is the result of a collective effort. I want to express my deep gratitude to the contributors of the Kaspa community, whose articles, research, and discussions have formed the backbone of this book. Much of the content has been adapted and translated from the invaluable resources available on the official website Kaspa.com/learn-kaspa and the writings of its main researchers and developers. Special thanks are also extended to Cihan0x.ETH (@cihan0xeth), whose work is partly based on the original analyses of @AbiKaspa, and to BankQuote_DAG for their insightful analyses that have greatly enriched this work.
Prepare to dive into one of the most innovative architectures in the world of cryptocurrencies. Prepare to understand Kaspa.
Table of Contents
- Chapter 1: Kaspa's BlockDAG
- Chapter 2: Kaspa - Linking the Body to the Header
- Chapter 3: Kaspa and the "Bitcoin Scalability Problem"
- Chapter 4: MuHash
- Chapter 5: Kaspa's UTXO Model
- Chapter 6: Parents vs Mergeset
- Chapter 7: Second Order Pruning
- Chapter 8: Kaspa GHOSTDAG Simplified
- Chapter 9: DAG Terminology
- Chapter 10: First Order Pruning
- Chapter 11: Archive Nodes vs Full Nodes
- Chapter 12: Kaspa: An Evolution in Energy-Efficient Decentralized Architecture
- Chapter 13: Kaspa vs Bitcoin Ordering
- Chapter 14: Kaspa's Vision for Layer 2: ZK Rollups and Bridging
- Chapter 15: The Igra Network: A Case Study of Kaspa's EVM-Compatible ZK Rollup
- Chapter 16: Transaction Throughput and Collisions in Kaspa's BlockDAG
- Chapter 17: Kaspa's Fee Market: A Game Theoretical Perspective
- Conclusion
- Appendix A: Additional Resources
- Appendix B: Mathematical Analysis of Transaction Collisions (Simplified)
- Appendix C: Mathematical Analysis of the Fee Market (Simplified)
Chapter 1: Kaspa's BlockDAG
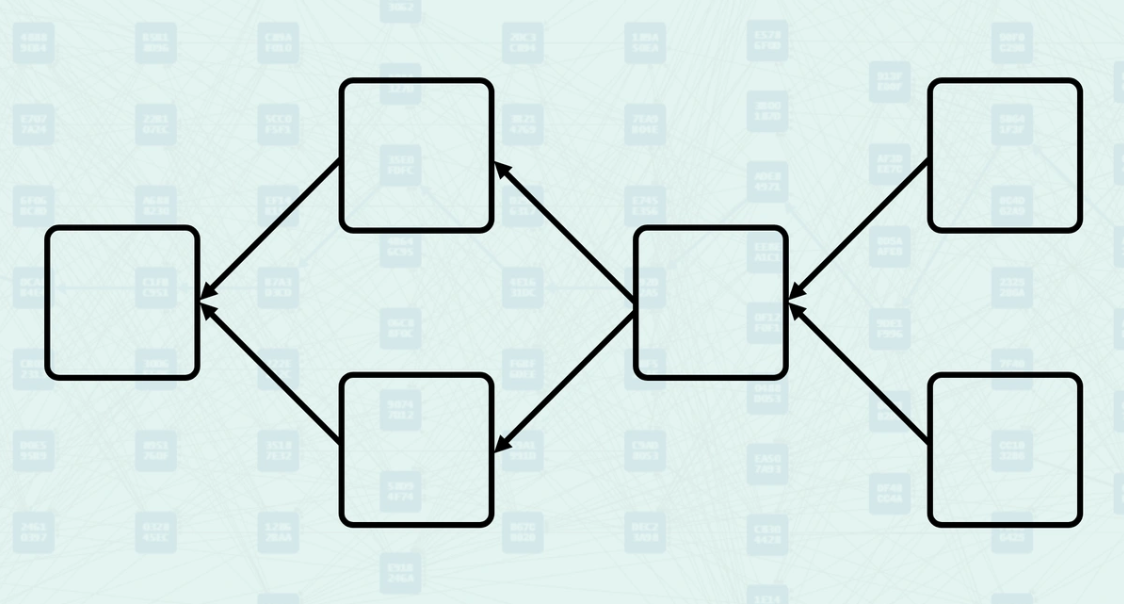
DAG - Directed Acyclic Graph
You've probably heard that Kaspa is a BlockDAG, but what does that mean? This article is designed to assume no prior knowledge, so we'll start with graph theory. We'll first look at what a Graph is, then what a Directed Graph is, then we'll get to the Directed Acyclic Graph, and finally how this applies to both Bitcoin and Kaspa.
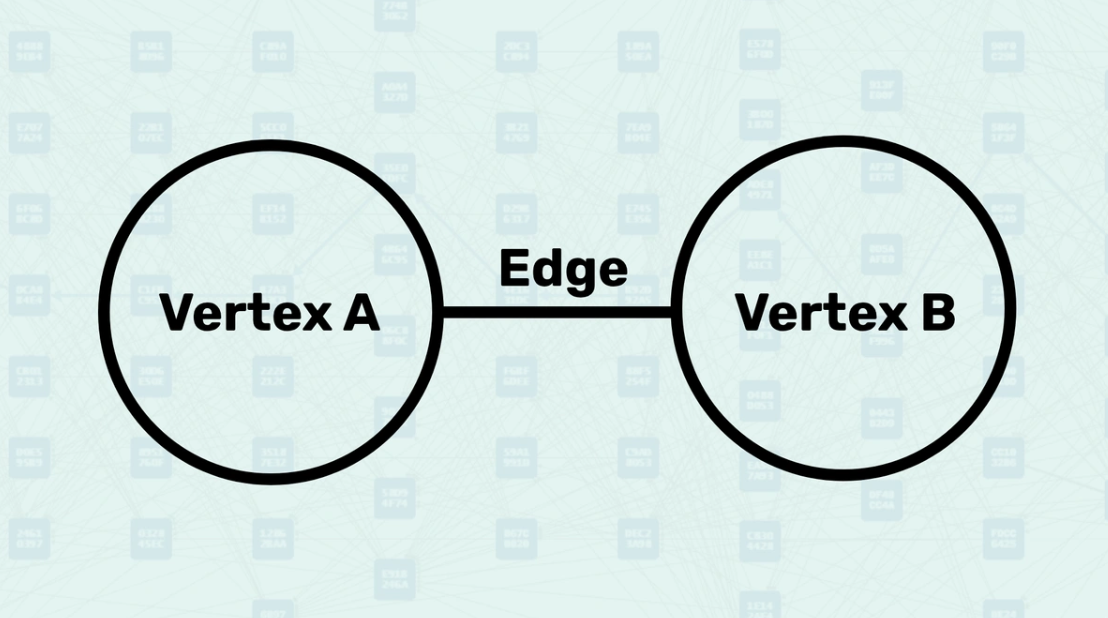
Graph - Graph theory, a field of mathematics and computer science, focuses on the study of graphs, which are structures representing relationships between pairs of entities. These graphs consist of vertices (also called nodes or points) connected by edges (sometimes called links or lines). Graphs are classified into undirected graphs, where connections between vertices are mutual, and directed graphs, where connections have a specific direction. As a key area of discrete mathematics, graph theory explores these structures in depth. The following image illustrates a simple undirected graph where connections have no direction.
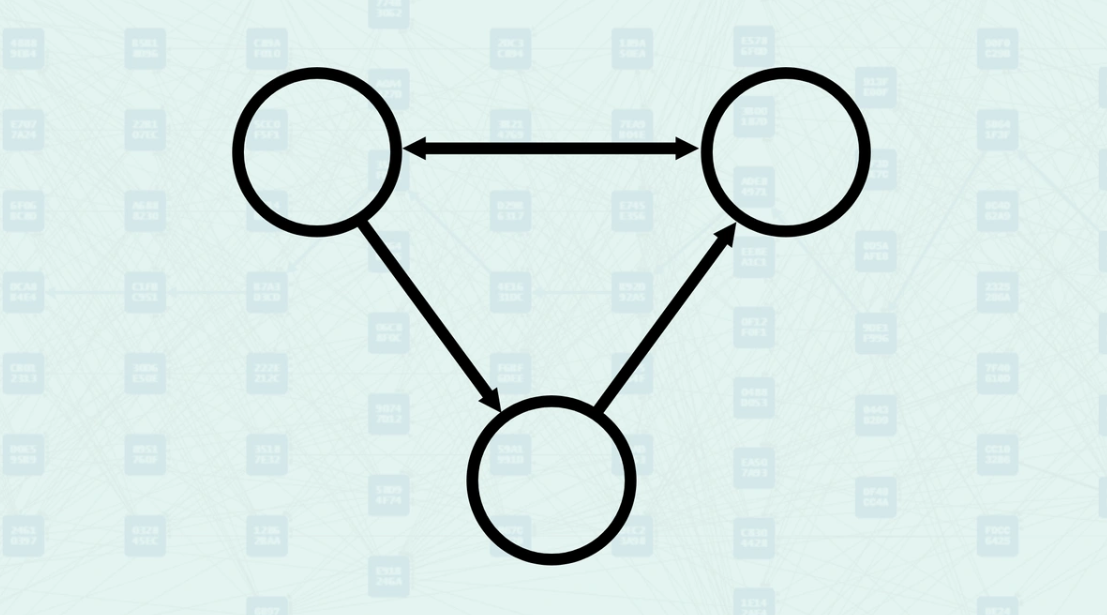
Directed Graph - A directed graph, often called a digraph, is a structure used to show relationships where connections between points have a specific direction. Unlike regular graphs where connections go both ways, in a directed graph, each edge points from one vertex to another. In its simplest form, a directed graph consists of two main parts: a collection of vertices and a set of edges, where each edge is a pair of vertices with a clear direction (from one vertex to another, but not vice versa). For example, if you have an edge from vertex X to vertex Y, X is the starting point and Y is the ending point. This edge connects X to Y. A different edge could go from Y to X, but that would be a distinct connection. In this basic configuration, called a simple directed graph, you cannot have multiple edges with the same direction between the same two vertices, nor can you have an edge that starts and ends at the same vertex (called a loop). The following image illustrates a directed graph where the edges have a direction; note that the edge with two pointers represents two edges, each with a direction.
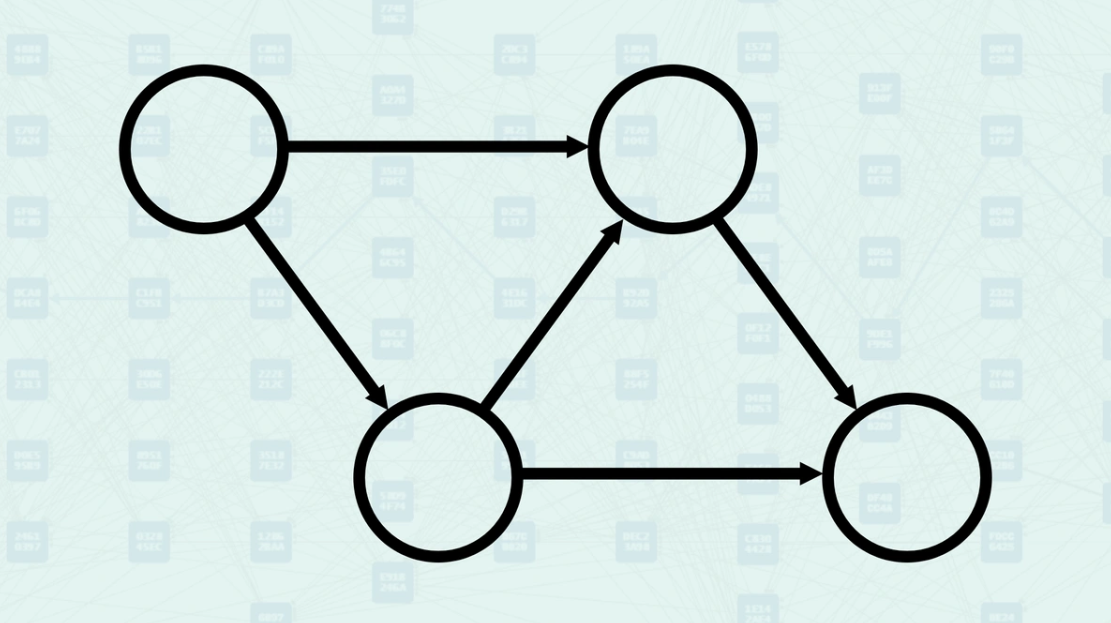
Directed Acyclic Graph - is a directed graph that contains no cycles. It is composed of vertices and edges, where each edge has a direction from one vertex to another, ensuring that following the directions of the edges never leads to a closed loop. A directed graph is called a DAG if its vertices can be arranged in a linear sequence that respects the direction of all edges, known as a topological order. The following image illustrates a directed acyclic graph where no cycle (or loop) can be found.
Simplified Definitions
Graph - consists of vertices and edges that connect pairs of vertices, where vertices represent any type of object and edges represent the connections between them.
Directed Graph - each edge has a specific direction, pointing from one vertex to another. A path in a directed graph is a sequence of edges where the ending vertex of one edge is the starting vertex of the next edge in the sequence.
Directed Acyclic Graph - a directed graph where no vertex can reach itself via a path that includes one or more edges, ensuring the absence of cycles.
There's a lot more to learn about graphs, but for our purposes, we only need to know that Kaspa's BlockDAG is just a structure, composed of edges and vertices, connected in a single direction, and that we never end up in a cycle, it is acyclic, or a Directed Acyclic Graph.
Bitcoin and Kaspa
Bitcoin - is a DAG, even though it is always called a Blockchain, Bitcoin uses the DAG structure. Blocks are vertices, and their relationship is that of edges. Each block is connected in a single direction and by following each connection, you will never make a cycle, and you will always return to the Genesis.
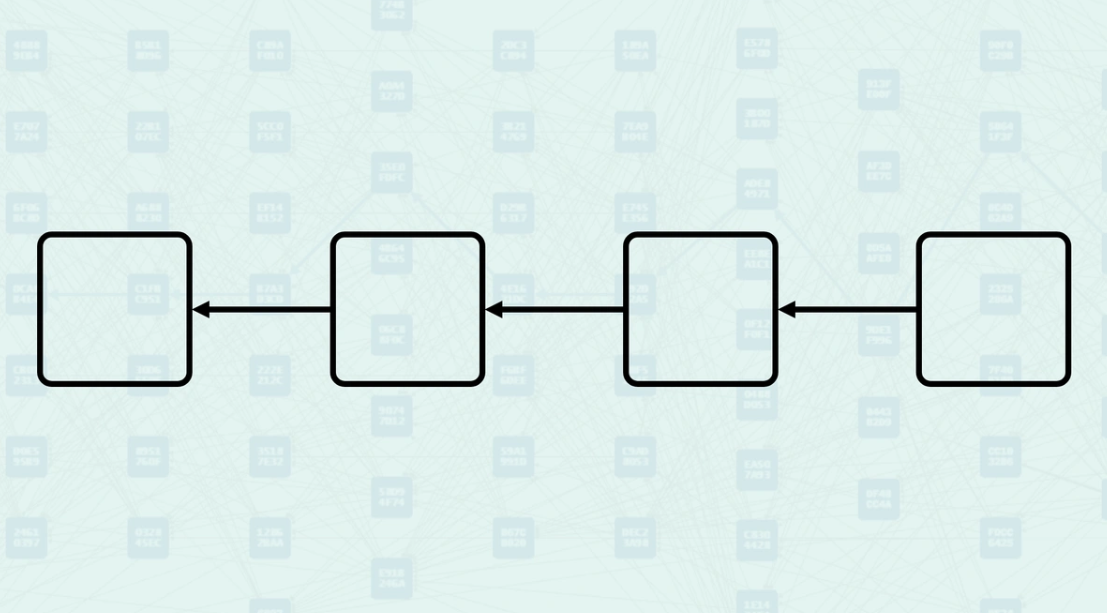
Kaspa - is a DAG, Kaspa uses the DAG structure. Blocks are vertices, and their relationship is that of edges. Each block is connected in a single direction and by following each connection, you will never make a cycle, and you will always return to the Genesis.
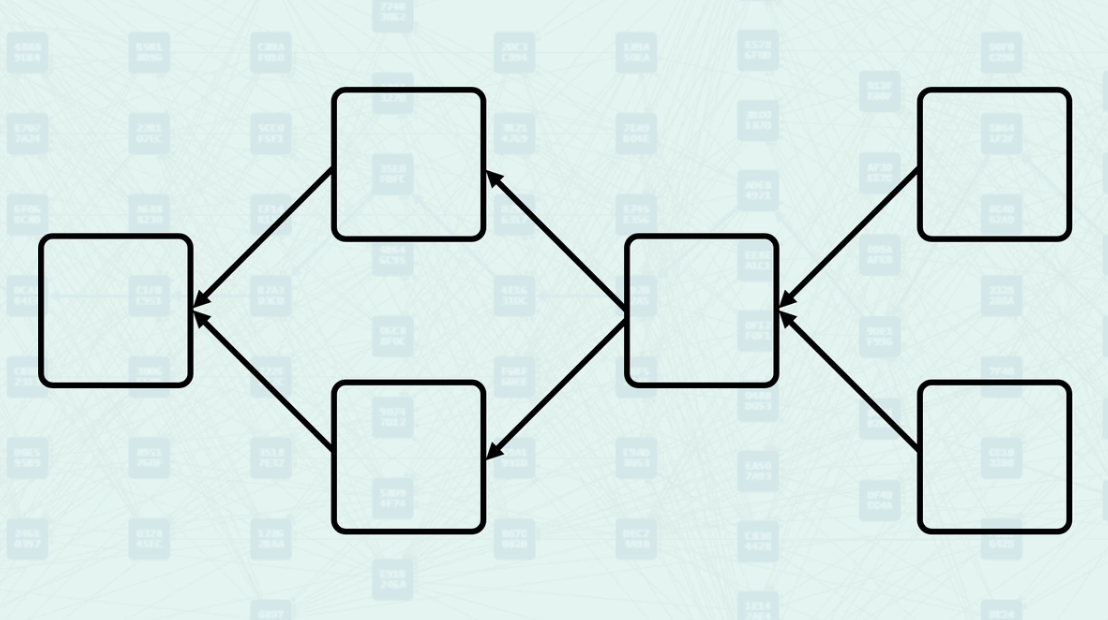
So, what's the difference if both Bitcoin and Kaspa use a DAG? Bitcoin allows blocks to point to only one previous block. Kaspa allows blocks to point to multiple previous blocks. This is the only difference in structure.
Chapter 2: Kaspa - Linking the Body to the Header
Securing the Block Body to the Header - Merkle Root
What secures the block body to the header? The Merkle Root of the transactions in the body.
What does that mean? This article is designed to assume no prior knowledge, so we'll start with a Merkle Tree. What is a Merkle tree, how it is built, and how it prevents tampering. Then, how it applies to both Bitcoin and Kaspa.
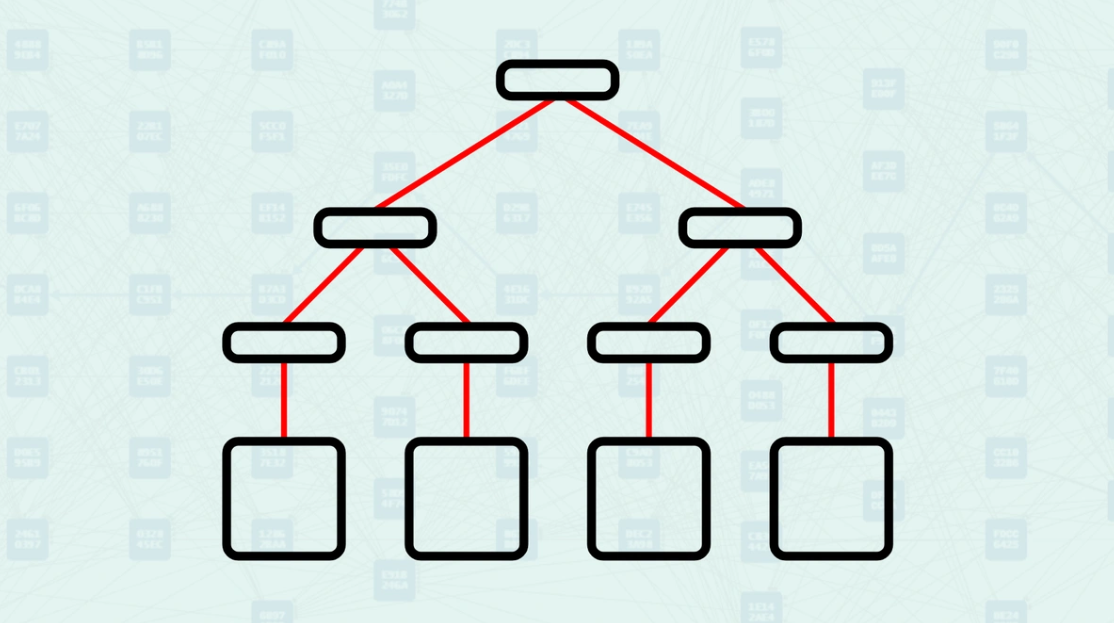
Merkle Tree - In cryptography and computer science, a Merkle Tree, also known as a Hash Tree, is a tree-like structure where each "leaf" node contains the cryptographic hash of a data block. Non-leaf nodes, often called branches or internal nodes, contain the cryptographic hash of their child nodes' labels. This structure allows for efficient and secure validation of the content of large data sets.
Data Block - In a Merkle tree, a data block is a segment of raw data, such as a transaction, that forms the basis of the tree structure. Each data block is individually hashed to produce a leaf node hash.
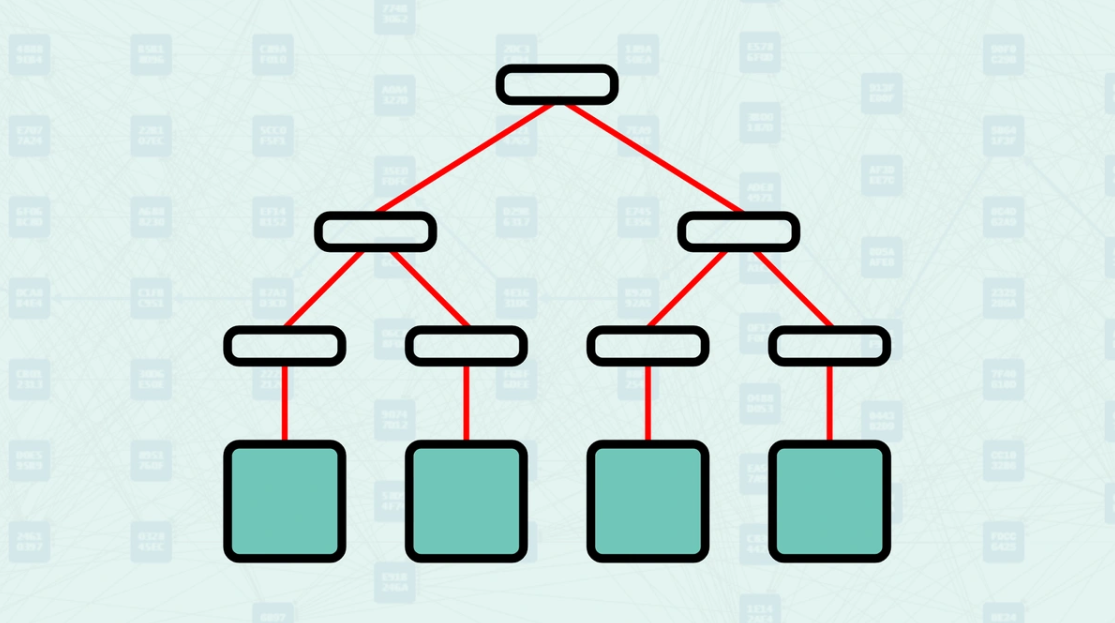
Leaf - A node in a Merkle tree that stores the cryptographic hash of a single data block. The leaf node, by storing this hash, acts as a digital fingerprint of the data block.
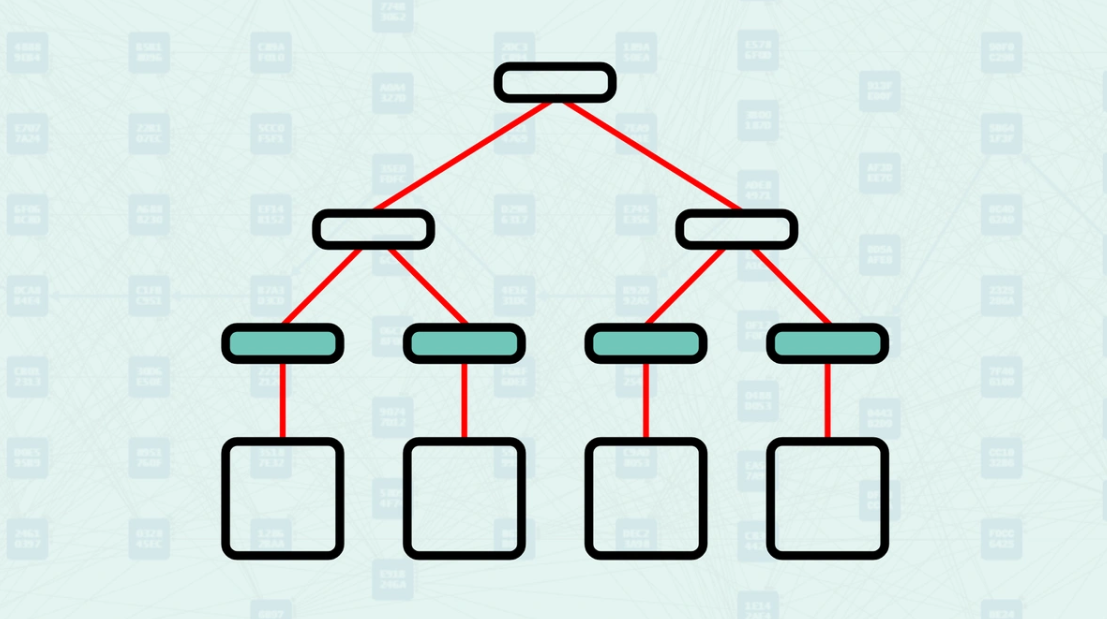
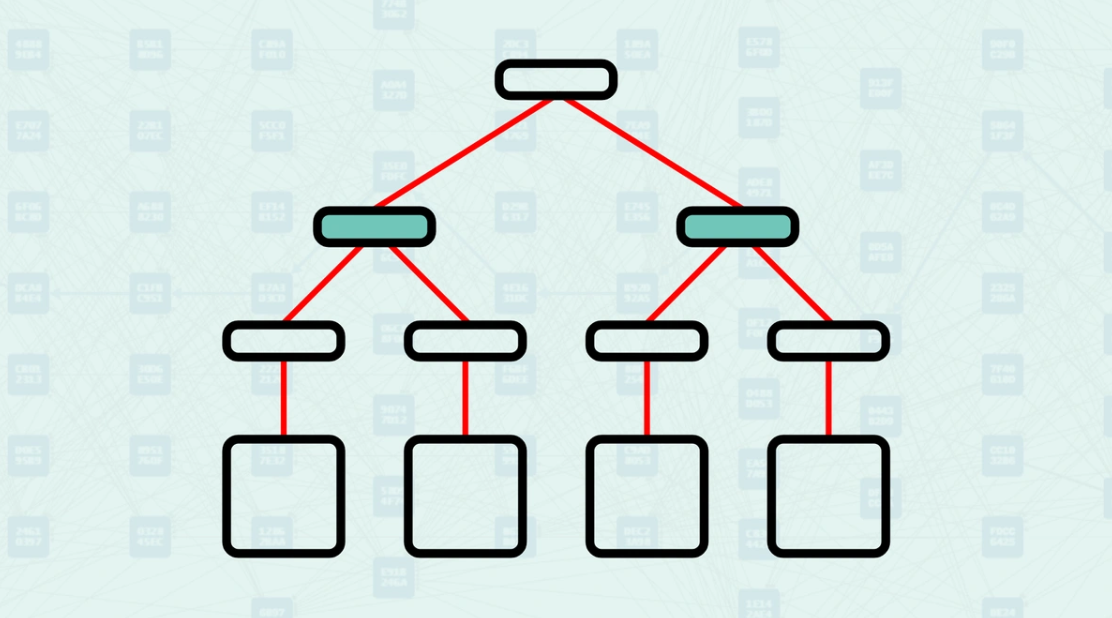
Internal Node - A parent node that aggregates the hashes of its child nodes. These child hashes are concatenated and hashed to produce a single hash value that labels the internal node.
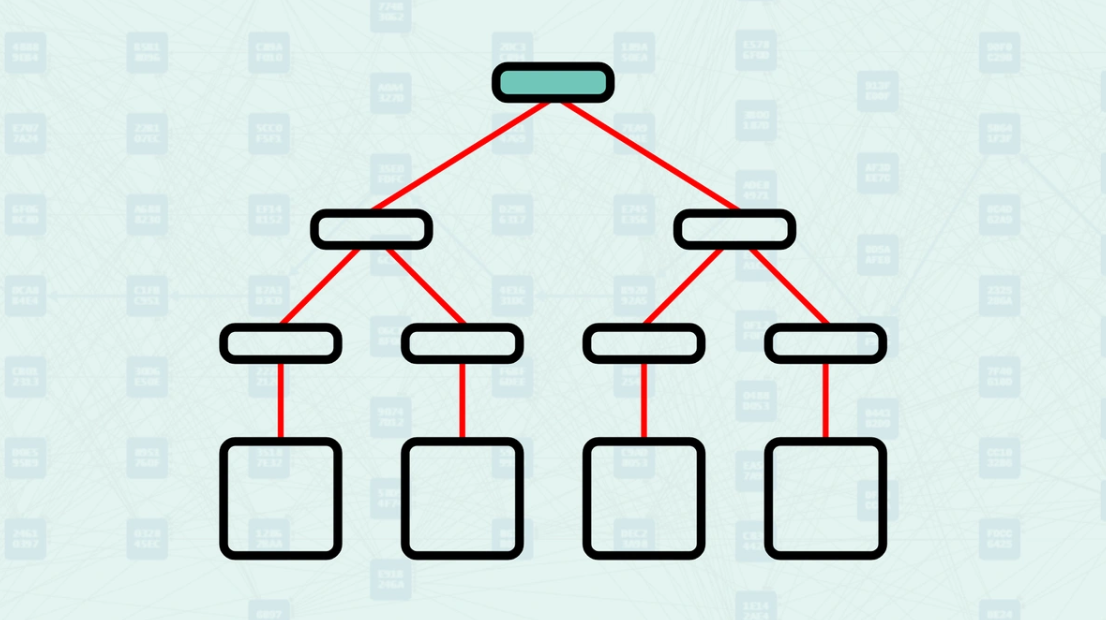
Hash Root - The singular hash value at the highest node, encapsulating all the data in the tree. It serves as a compact and unique summary of all underlying data blocks. Any modification to a single leaf node alters the hash root.
Simplified Definitions
Merkle Tree - A tree-like structure used to efficiently verify data integrity by organizing data blocks into a structure of cryptographic hashes.
Data Block - A unit of information, such as a transaction, that is hashed to create a leaf node.
Leaf - A node that stores the hash of a single data block.
Internal Node - A parent node that contains the hash of its child nodes.
Hash Root - The highest node containing a single hash that represents the integrity of the entire data set.
Bitcoin and Kaspa
Bitcoin - a Merkle Tree organizes transaction data within each block. Transactions are hashed into leaf nodes, paired and hashed into internal nodes, and combined into a single hash root stored in the block header. This structure allows for efficient verification of transaction integrity.
Kaspa - a Merkle Tree organizes transaction data within each block in the same way as Bitcoin. However, Kaspa allows for the coexistence of parallel blocks, where the order between these blocks in the DAG cannot be known. A Merkle Tree depends on order. How does Kaspa solve this? By adding an additional Merkle Tree.
What secures the block body to the header? The Merkle Root of the transactions in the body (hash_merkle_root).
What secures the mergeset transactions to the header? The Merkle Root of the transactions in the mergeset (accepted_id_merkle_root). This second root allows for the validation of transactions from parallel blocks that are merged, thus solving the ordering problem in a DAG environment.
Chapter 3: Kaspa and the "Bitcoin Scalability Problem"
Kaspa solved the "Bitcoin Scalability Problem" - What is it?
What is the Bitcoin Scalability Problem and how did Kaspa solve it? Through inclusion.
What does that mean? This article is designed to assume no prior knowledge, so we'll start with a Client-Server Model, then the Peer-to-Peer network. What is a P2P network, what it looks like, and how messages propagate within it. Then, how it applies to both Bitcoin and Kaspa.
Client-Server Model - In a client-server network, a centralized architecture organizes communication and resource sharing via a single powerful computer called a server, which connects to multiple user devices called clients. This structure ensures efficient management but relies heavily on the server, making it vulnerable.
Peer-to-Peer (P2P) Network - A decentralized architecture that allows direct communication and resource sharing between interconnected nodes. Each peer functions as both a client and a server, contributing to the network's resilience and scalability without relying on a central authority.
Propagation Time - In a P2P network, propagation time is the duration it takes for data (like a new block) to travel from one node to others across the network. During this time, different nodes may have different views of the network's state.
Simplified Definitions
Client-Server Model - A central computer manages data for multiple clients.
Peer-to-Peer (P2P) - Multiple computers share data directly with each other without a central authority.
Node - A single computer participating in a P2P network.
Propagation Time - The time it takes for data to propagate across the network.
Bitcoin and Kaspa
Bitcoin - Uses a P2P network. However, its security depends on the block creation rate (10 minutes) being much slower than the propagation time. If blocks are created too quickly, many blocks are "orphaned" (rejected), which wastes work and compromises security. This is the "scalability problem."
Kaspa - Uses an inclusive protocol (GHOSTDAG) that allows blocks to point to multiple previous blocks. If parallel blocks are created during propagation time, they are all included in the DAG. There are no orphaned blocks. This allows the block creation rate to be faster than the propagation time, thus solving the scalability problem while maintaining security.
Chapter 4: MuHash
What is MuHash and how does Kaspa use it?
A structure for tracking UTXOs and pruning old block body data.
What does that mean? This article is designed to assume no prior knowledge, so we'll start with MuHash. What is a MuHash structure, how it is calculated, and how it preserves the properties of Multiplication. Then, how it applies to both Bitcoin and Kaspa.
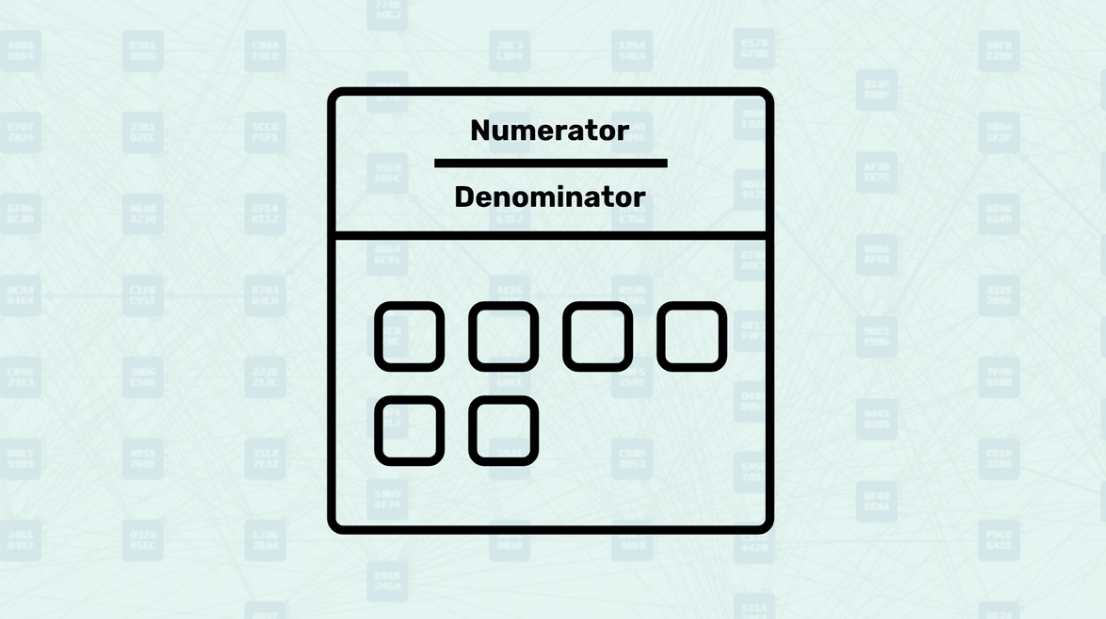
MuHash - In cryptographic systems, MuHash (Multiplicative Hash) is a specialized hashing algorithm designed to efficiently compute a single hash value from a set of elements. It allows for incremental updates, meaning that elements can be added or removed without recalculating the entire hash, which improves performance in dynamic data sets.
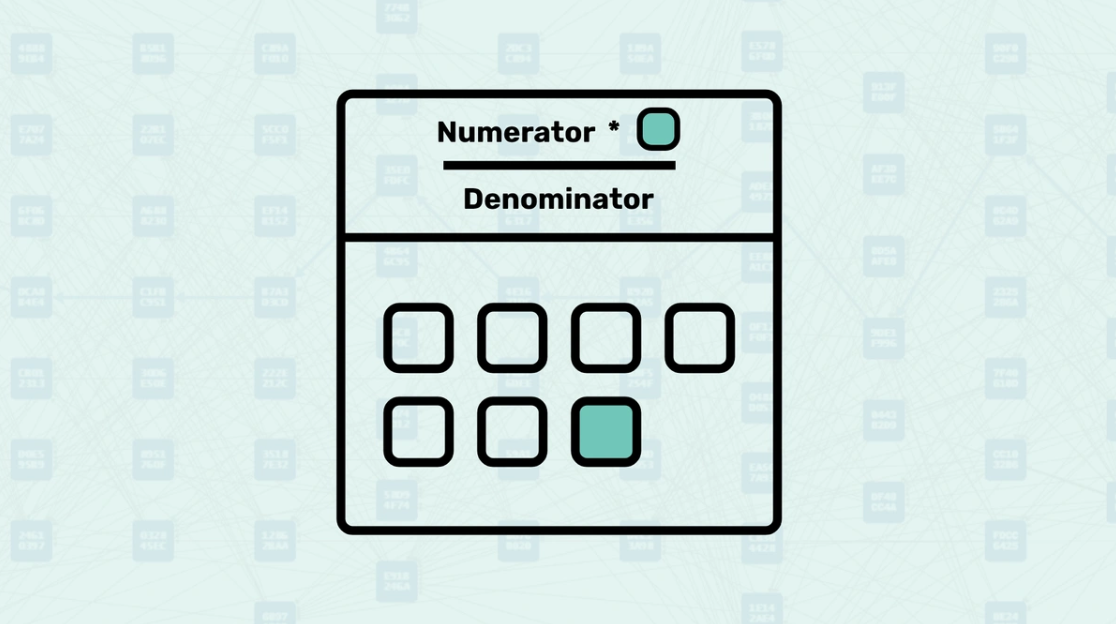
Numerator and Denominator - MuHash uses two counters: a numerator that multiplies added elements and a denominator that multiplies removed elements. The final state is obtained by "dividing" the numerator by the denominator (via multiplication by the modular inverse). The order of operations does not matter, which is crucial for parallel processing.
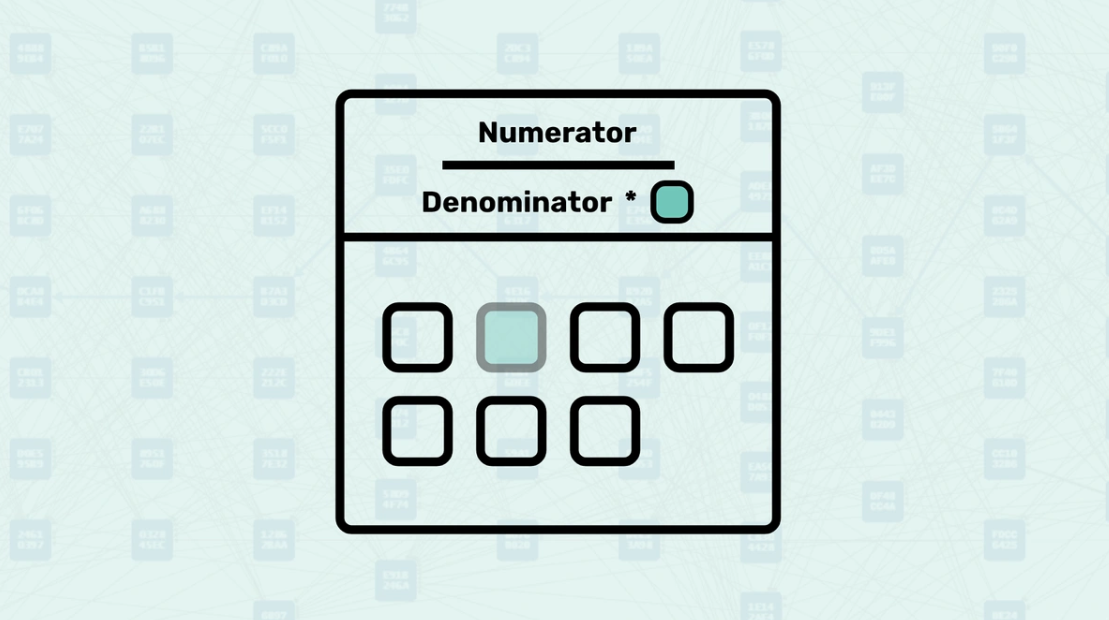
Prime Modulo Constraint - The modular prime number acts as a mathematical boundary that keeps both the numerator and denominator within a manageable range during all arithmetic operations. Each multiplication is performed modulo a prime number, meaning that no matter how many elements are added or removed, the results always "wrap around" to stay within the finite field.
Modular Inverse - The modular inverse is the mathematical operation that makes division possible in the finite field used by MuHash. When you need to "divide" the numerator by the denominator to get the final hash result, you actually multiply the numerator by the modular inverse of the denominator.
Simplified Definitions
MuHash - A structure for quickly hashing elements in a set, where order does not matter.
Numerator - The field where elements are multiplied when added.
Denominator - The field where elements are multiplied when removed.
Prime Modulo Constraint - A prime number that defines the mathematical field where all operations take place.
Modular Inverse - The operation that allows "division" in a finite field.
MuHash is just a structure, composed of a numerator and a denominator, that allows for fast hashing of elements in a set in any order without recalculating from scratch.
Bitcoin and Kaspa
Bitcoin - Full nodes retain all transactions, including old spent transactions. Pruning is difficult because there is no efficient mechanism to compactly and verifiably summarize the transaction state (the UTXO set) without retaining historical data.
Kaspa - Full nodes prune old data. This ability to prune old data requires a way to remove all transaction data from each block AND cryptographically secure it to each header. Kaspa uses MuHash to remove transaction data from blocks (so that only the DAG headers remain after the pruning point) and secure it to each header. This is an essential step for pruning. Kaspa separates Transaction Data (UTXO) from Consensus Data (Headers), meaning Kaspa only stores Unspent Transactions, instead of all transactions ever made. This reduces storage requirements compared to Bitcoin.
Chapter 5: Kaspa's UTXO Model
What is a UTXO and how does Kaspa use it?
A structure for tracking who can spend which Kaspa.
What does that mean? This article is designed to assume no prior knowledge, so we'll start with the Account Model and the UTXO model, then what a UTXO is, what it contains, and how it is spent. Then, how it applies to both Bitcoin and Kaspa.
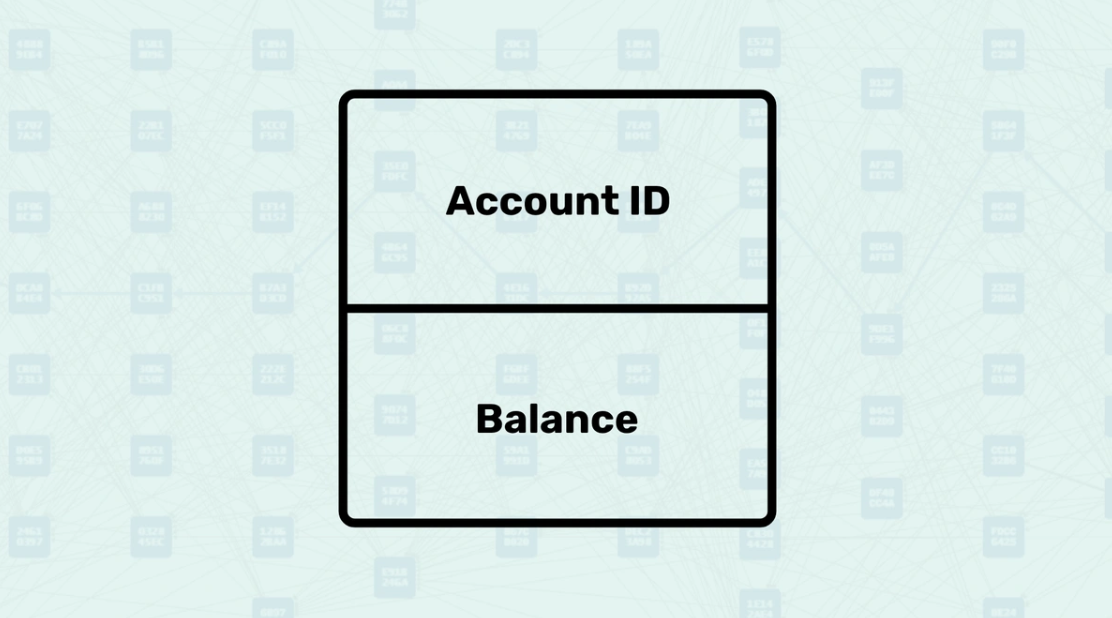
Account Model - The Account Model behaves like a traditional bank account by maintaining a balance and offering familiar operations. Just like checking your bank balance, you can query the account's current holdings, and similar to how banks track your transaction history, the Account manages your financial state. The system provides standard account operations such as receiving deposits and performing transfers, with each account having its own unique identifier and name for easy management. Several account types are available to meet different needs, just as banks offer various account types for different purposes.
UTXO Model - The UTXO Model behaves like physical cash or coins in your wallet, where each coin has a specific value and can only be spent once. Just as you might have multiple bills and coins of different denominations in your physical wallet, a digital wallet contains multiple UTXOs of varying amounts that represent your spendable balance. When you make a transaction, specific UTXOs are consumed as inputs (like spending exact bills), and new UTXOs are created as outputs for the recipient and any change returned to you, similar to how a cashier gives you change when you pay with a larger bill. The system tracks these individual "coins" across all transactions, maintaining a complete record of which UTXOs exist and can be spent, just as physical money moves from person to person while retaining its individual identity.
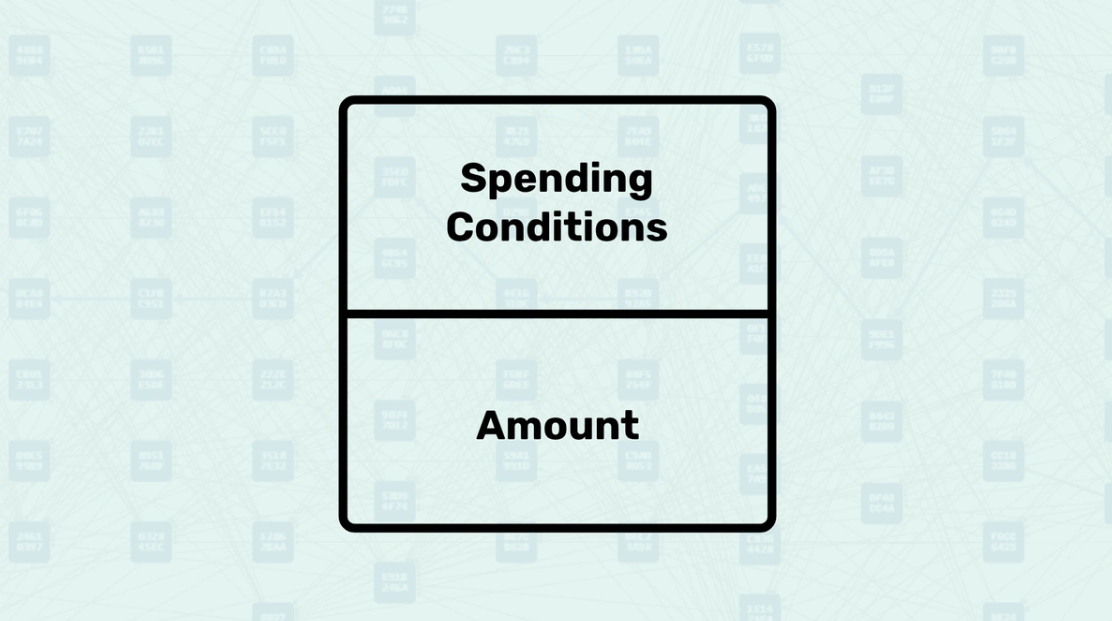
UTXO Structure - A UTXO (Unspent Transaction Output) is structured as a digital receipt that contains all the essential information needed to spend it, similar to how a check contains the amount, recipient details, and authorization information. Each UTXO contains the amount of value it holds and defines the spending conditions. Just as a physical coin has its denomination stamped and can be verified as authentic, each UTXO carries its value and cryptographic proof of ownership, making it a self-contained unit of value that can be verified and spent independently. The system treats each UTXO as a discrete object with its own unique identifier, allowing for precise tracking of individual value units as they move across the network.
Spending a UTXO - Spending a UTXO behaves like using physical cash, where you must present the exact bill or coin to make a purchase, and once spent, it cannot be used again. The process begins by locating the specific UTXO you wish to spend and verifying its existence in the UTXO set, similar to checking that a bill in your wallet is authentic and unspent. When creating a transaction, you reference the UTXO by its unique identifier and provide a signature script that proves you have the right to spend it. The system validates that the UTXO has not already been spent (preventing double-spending), verifies that you meet the spending conditions, and then removes the UTXO from the spendable set while creating new UTXOs as outputs, completing the transfer of value from one party to another.
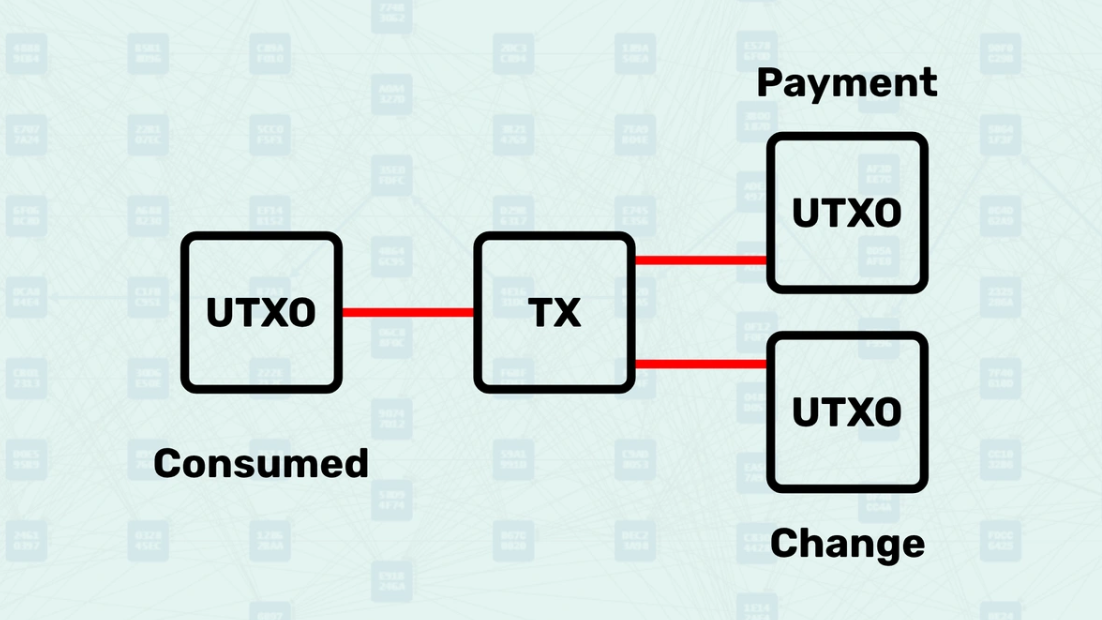
Simplified Definitions
Account Model - A system that maintains a single balance per account.
UTXO Model - A system that tracks individual "coins" of value.
UTXO - An unspent transaction output, representing a specific sum of money.
Spending a UTXO - The process of consuming a UTXO to create new UTXOs.
A UTXO is just a structure for tracking who can spend what.
Bitcoin and Kaspa
Bitcoin - Uses the UTXO model. Transactions are collections of consumed and created UTXOs, stored in the body of each block.
Kaspa - Also uses the UTXO model. The main difference lies in how these UTXOs are managed and validated in a BlockDAG environment, which allows for parallel processing and faster confirmations.
Chapter 6: Parents vs Mergeset
What are Parents and Mergeset and how does Kaspa use them?
Two different ways to describe relationships between blocks in Kaspa's BlockDAG structure.
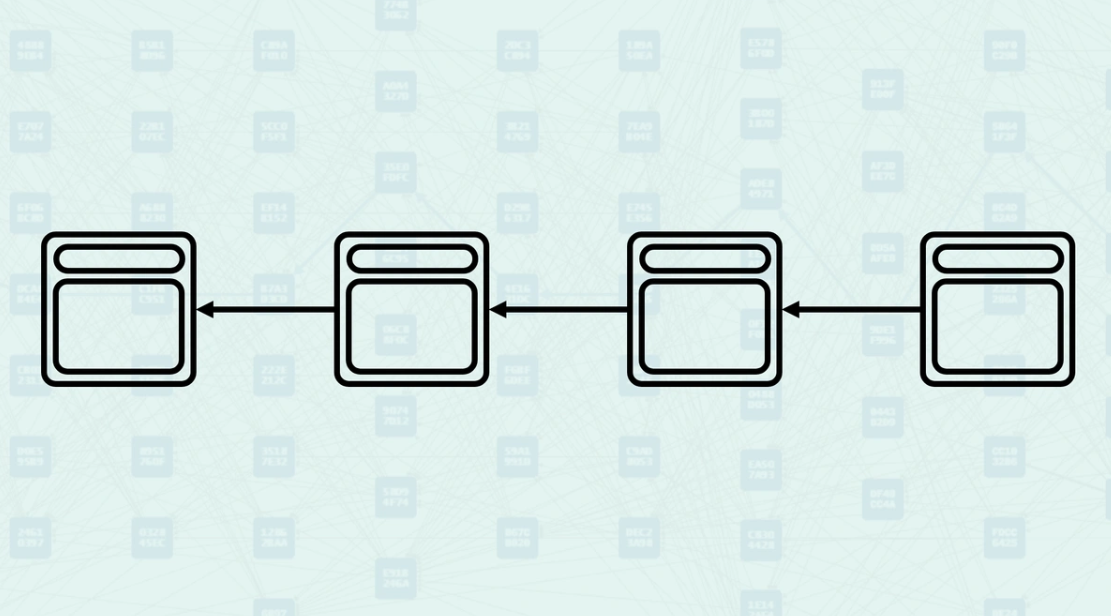
Traditional Blockchain Parents - In a linear blockchain like Bitcoin, each block has exactly one parent (except Genesis), creating a simple chain structure. The parental relationship is straightforward: each new block references the hash of the previous block, forming an unbroken sequence from Genesis to the current tip.
DAG Parents Complexity - Kaspa's BlockDAG allows blocks to have multiple parents, creating a more complex network of relationships. When a block is created, it can reference several existing blocks as parents, allowing for the creation of parallel blocks and higher throughput.
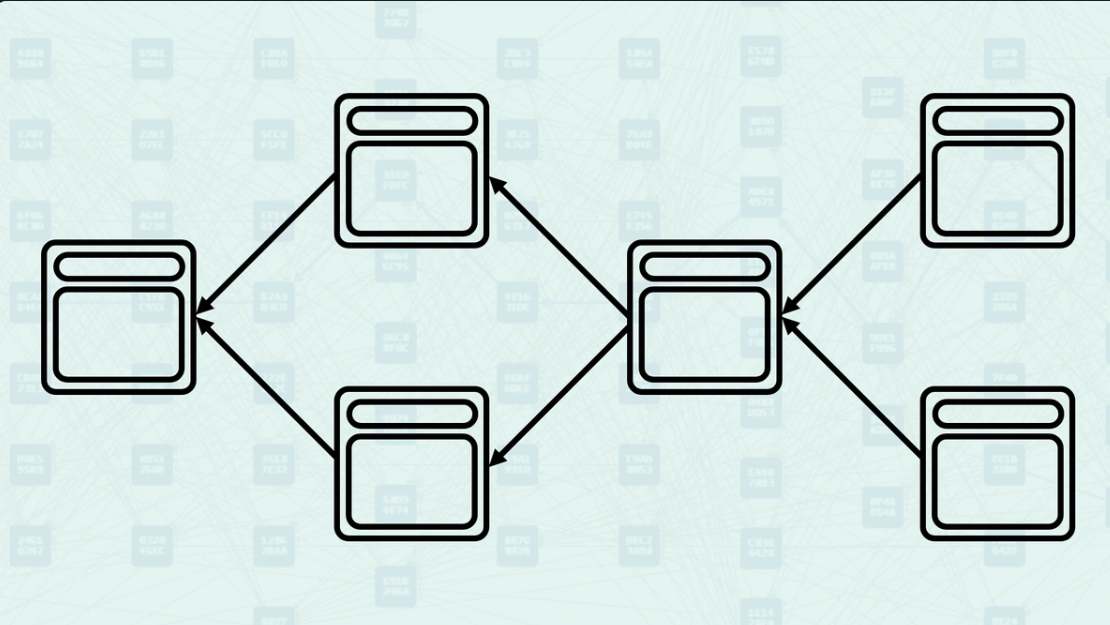
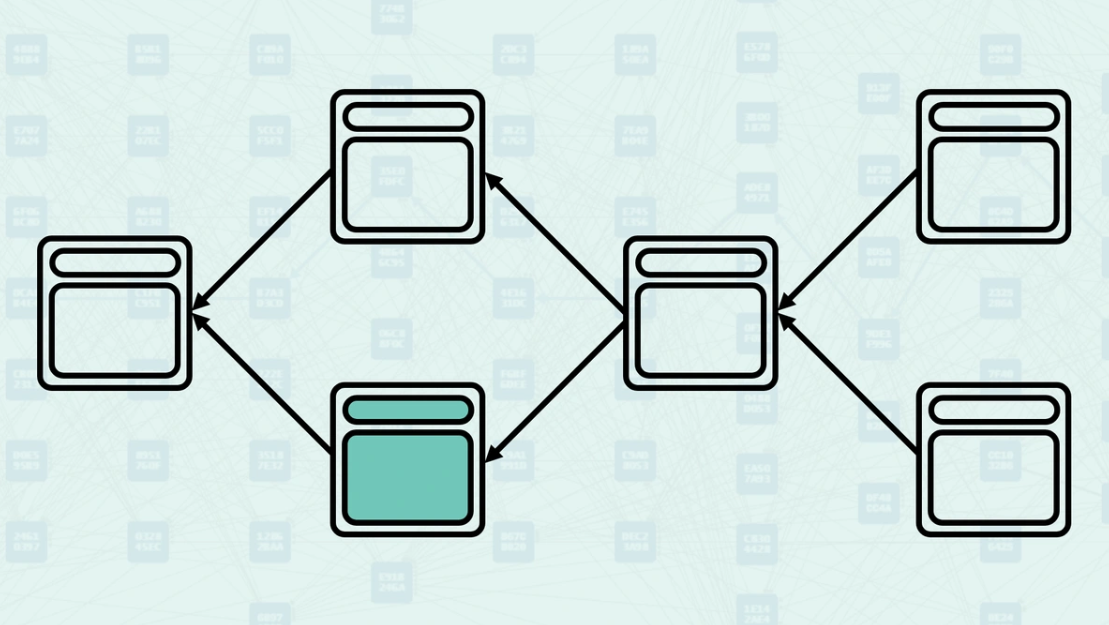
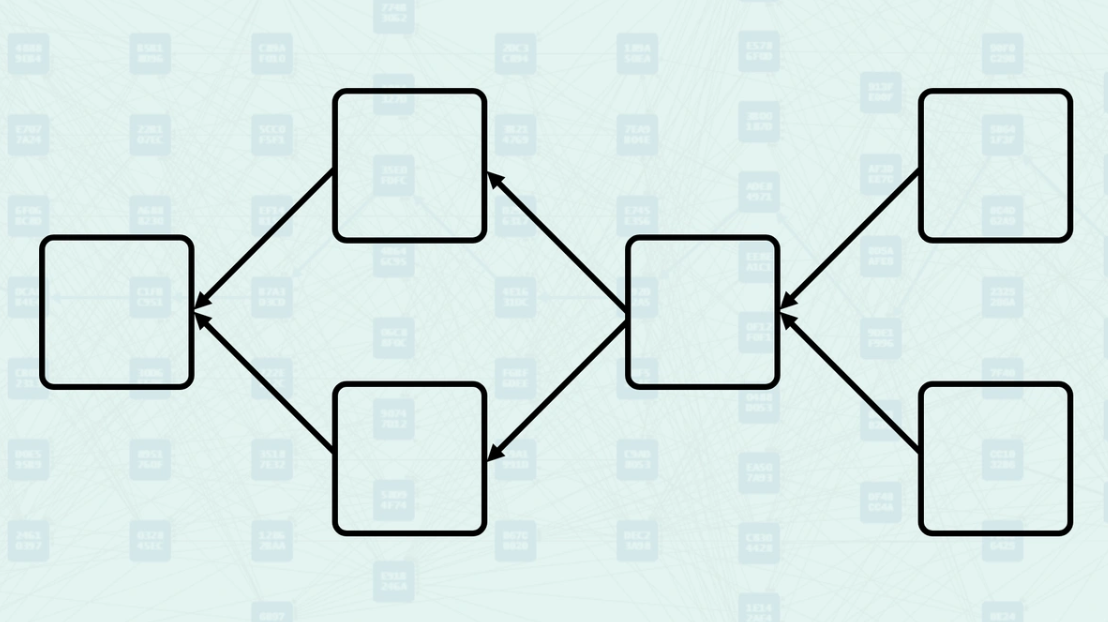
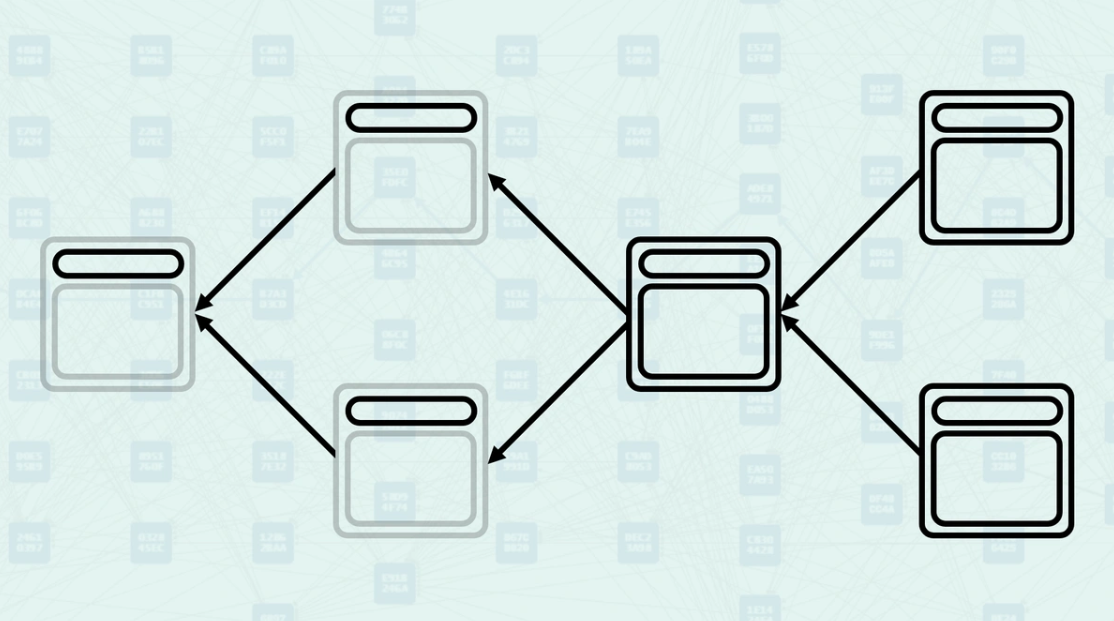
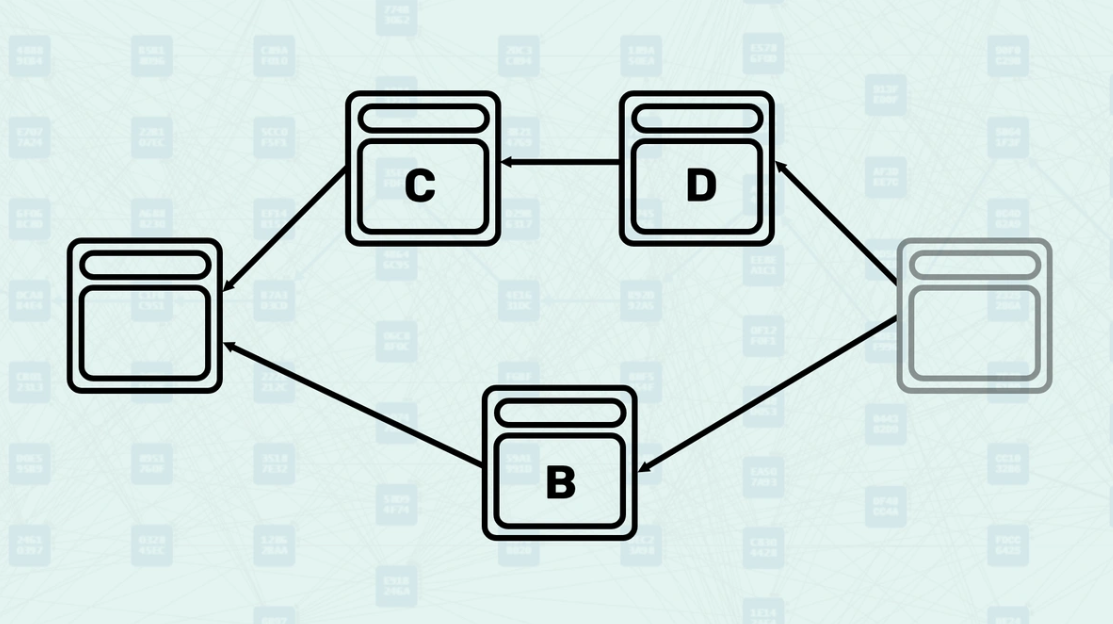
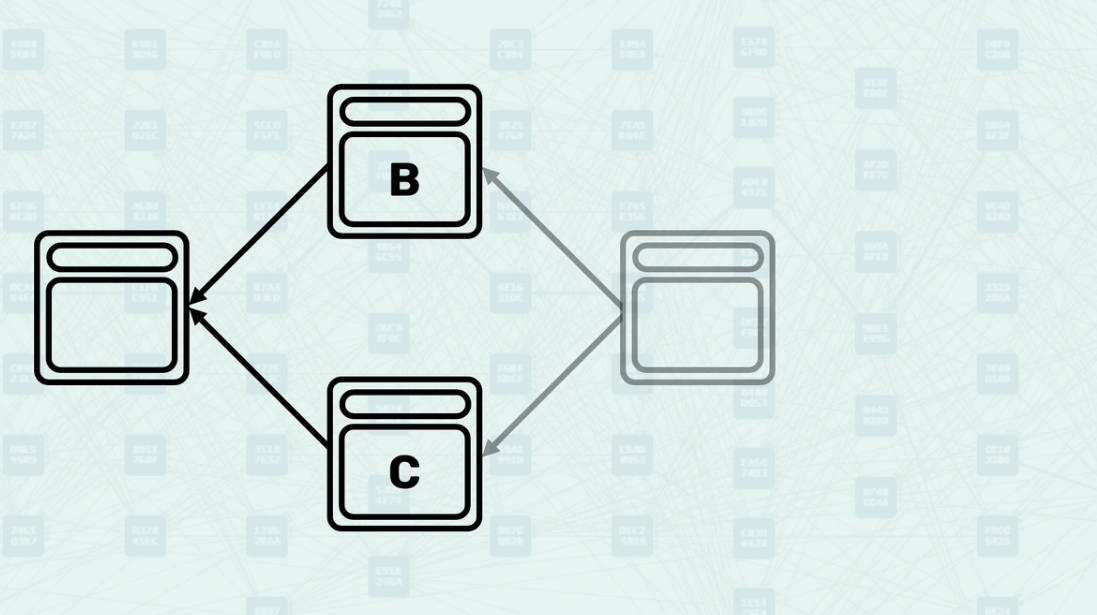
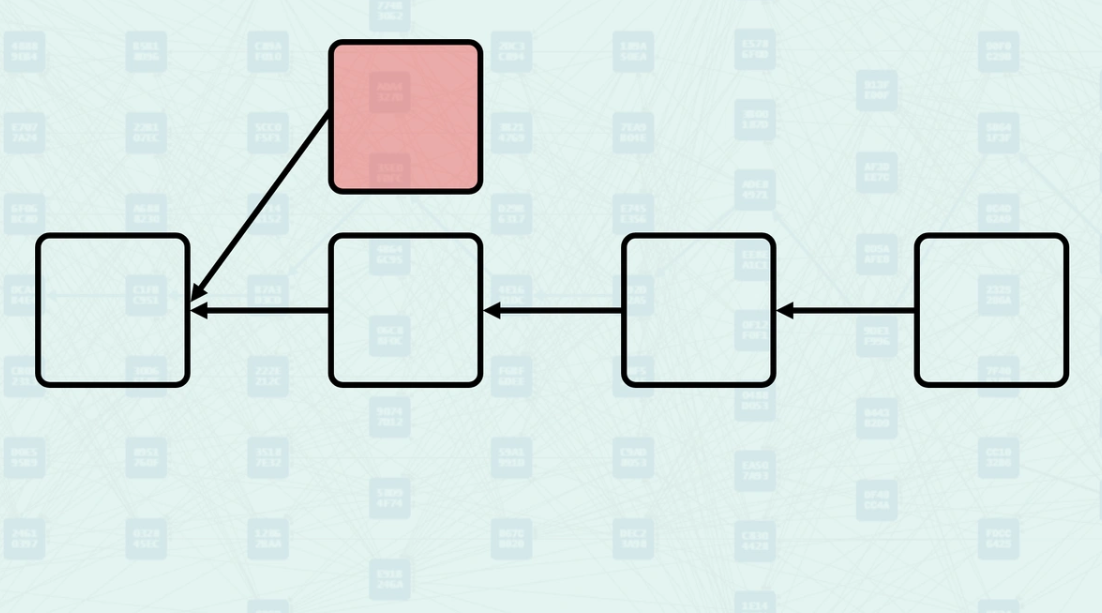
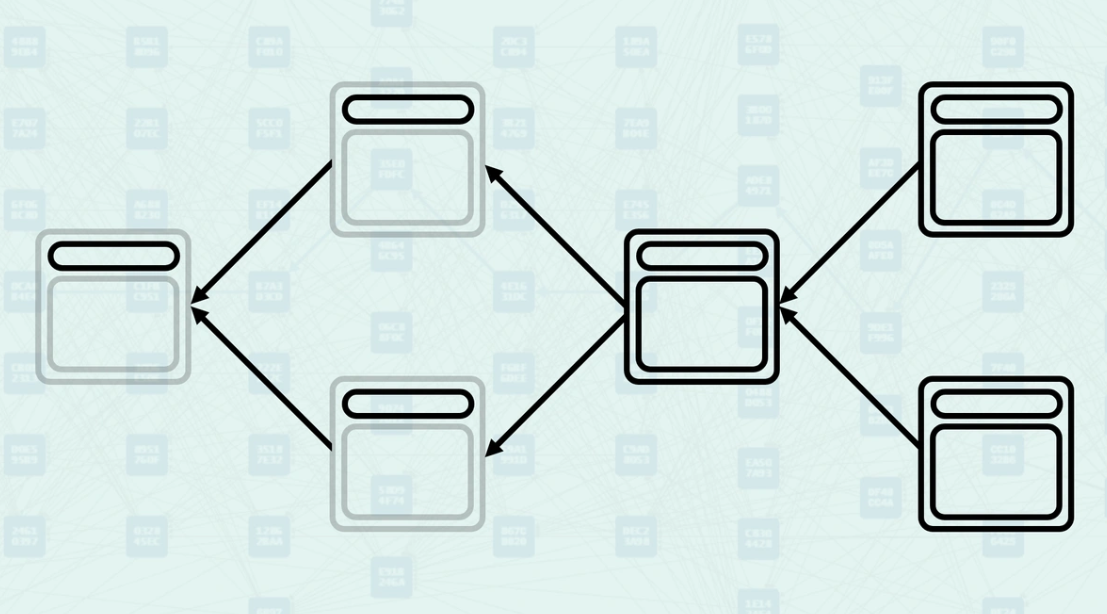
Parents - Parents are the blocks that a new block directly references in its header. These are explicit relationships declared by the block creator - they are the blocks that this new block directly builds upon. When you view a Kaspa DAG Visualizer, these arrows represent the parental relationship.
How Parents Work - When creating a block, miners select existing blocks to reference as parents based on what they consider the current "tips" of the DAG. The system validates these parental relationships and uses them to determine the block's position within the DAG structure. Here, you can see a new block being created, referencing the "tips" of the DAG, the blocks found without another block pointing to them.
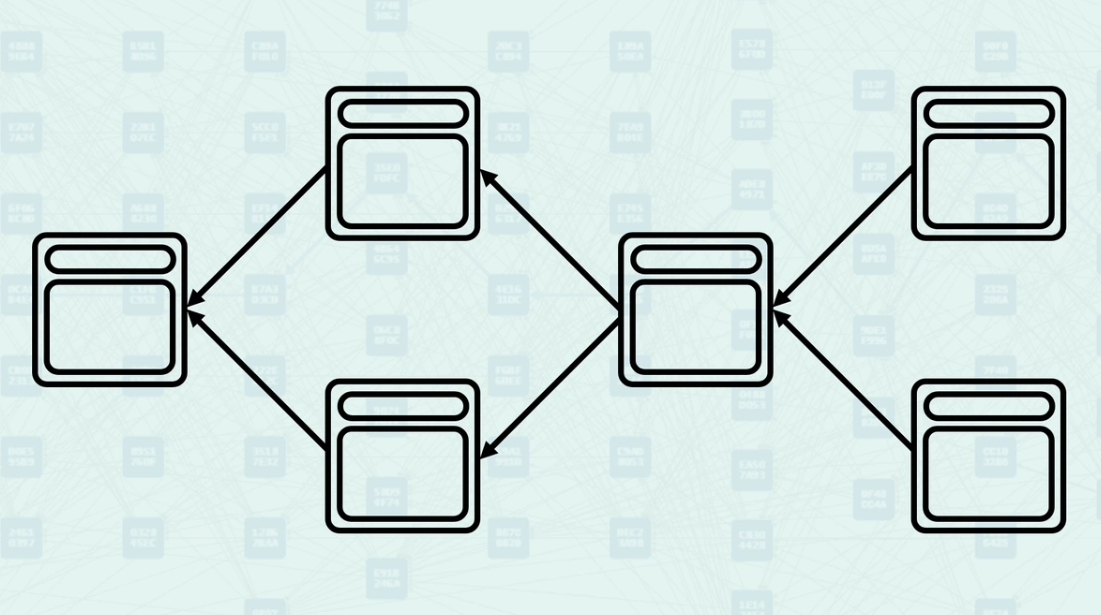
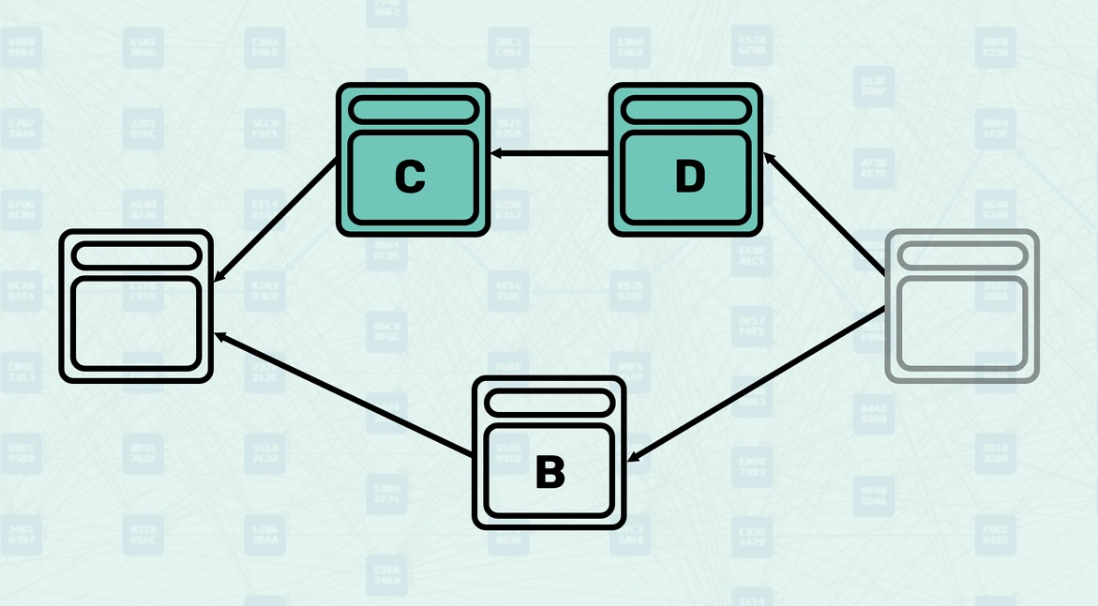
Mergeset - The mergeset is the set of blocks that are in the anticone of a block's selected parent but are still considered part of the block's consensus context. Here, block C is in the anticone of B, and block B is in the anticone of C.
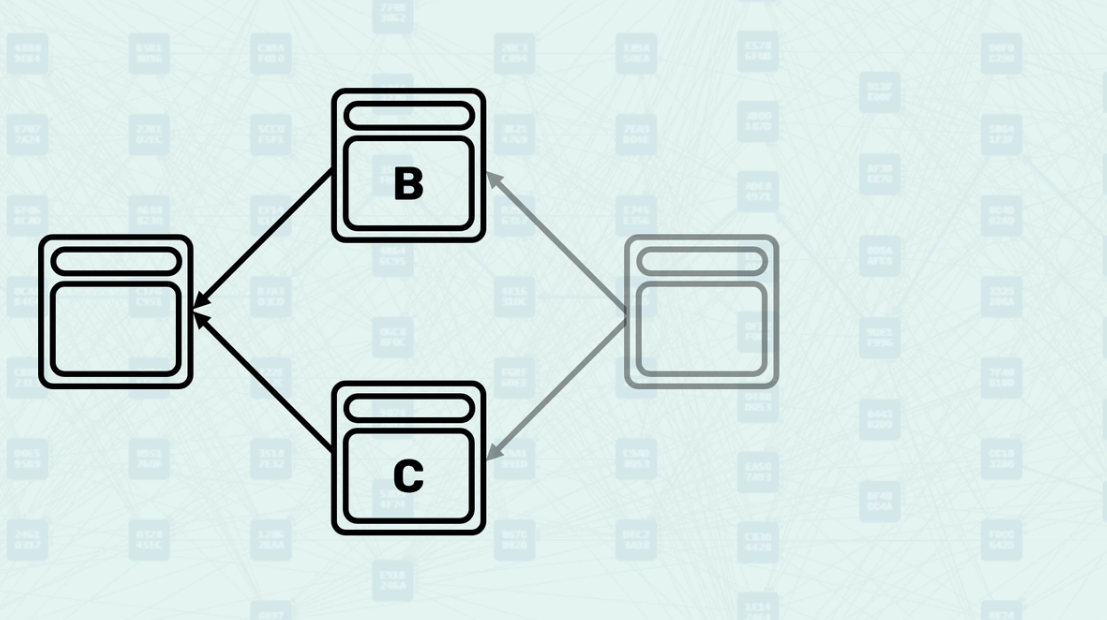
How the Mergeset is Calculated - The mergeset is calculated by finding all blocks that are not ancestors of the selected parent but are still reachable via the block's set of parents. This creates a broader context of blocks that must be considered for consensus decisions. In this example, if block B is the selected parent, the mergeset of the block being created would include both block C and block D.
Mergeset in GHOSTDAG - The GHOSTDAG protocol processes the mergeset to determine which blocks should be colored "blue" (contributing to consensus) or "red" (valid but not contributing). This coloring process is essential for maintaining consensus in the parallel block environment.
How Parents and Mergeset work together
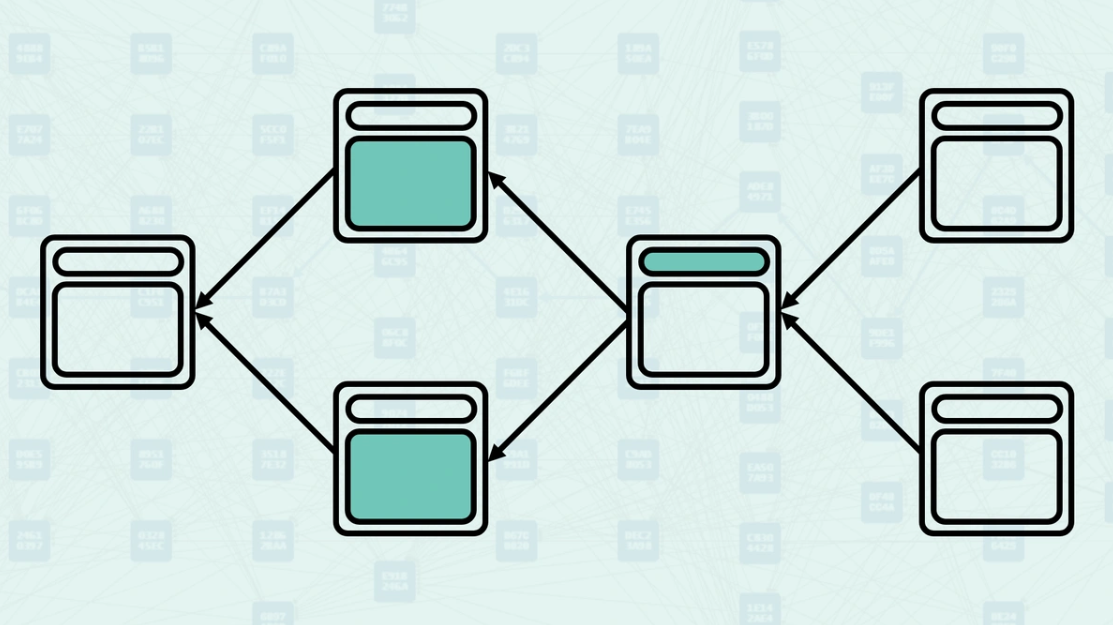
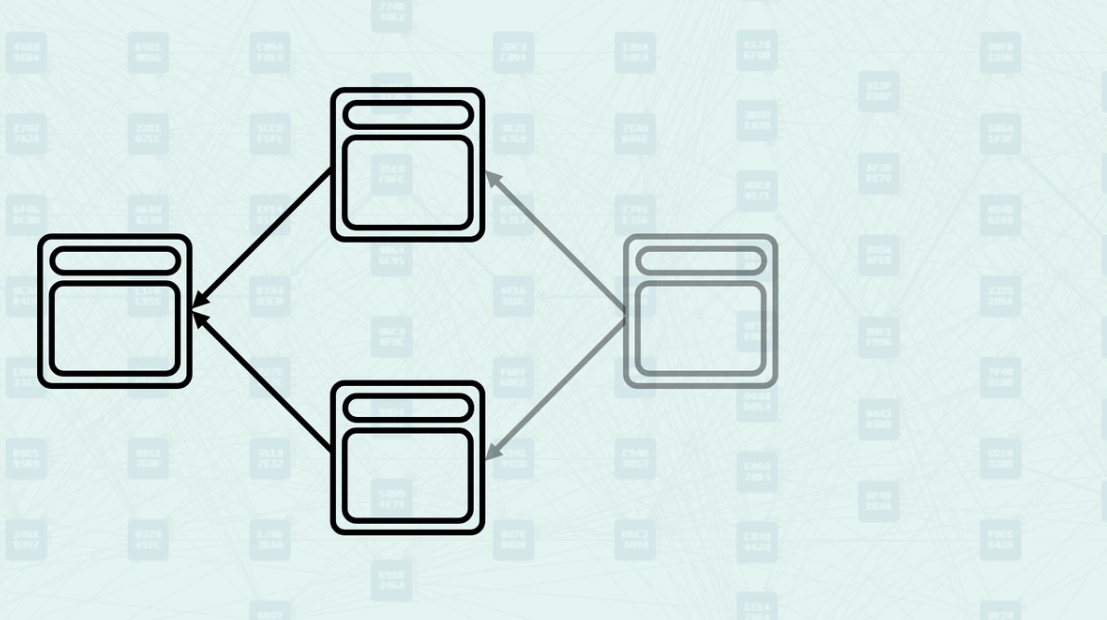
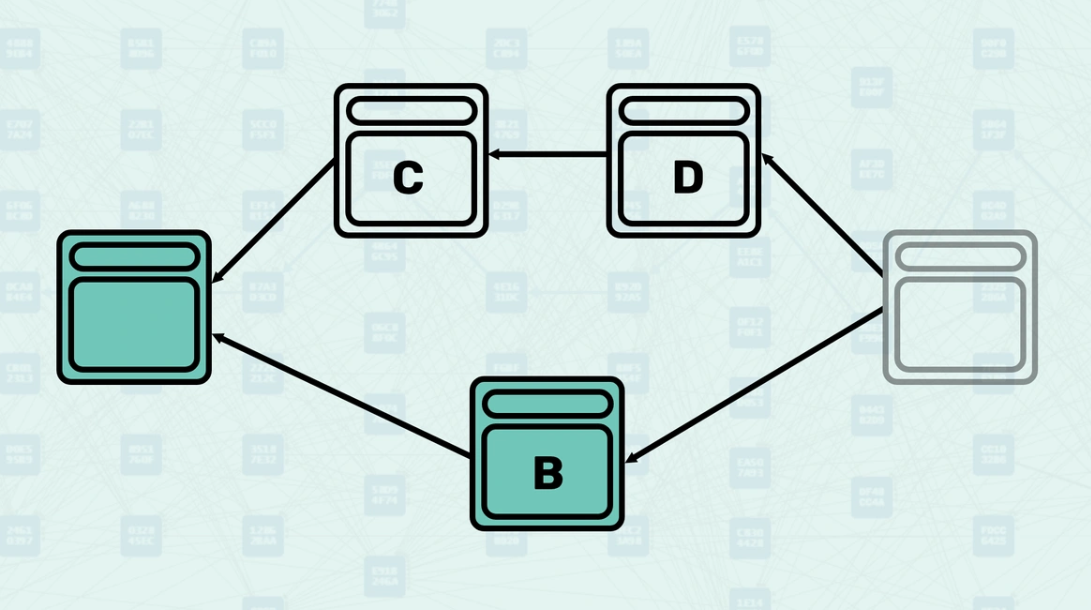
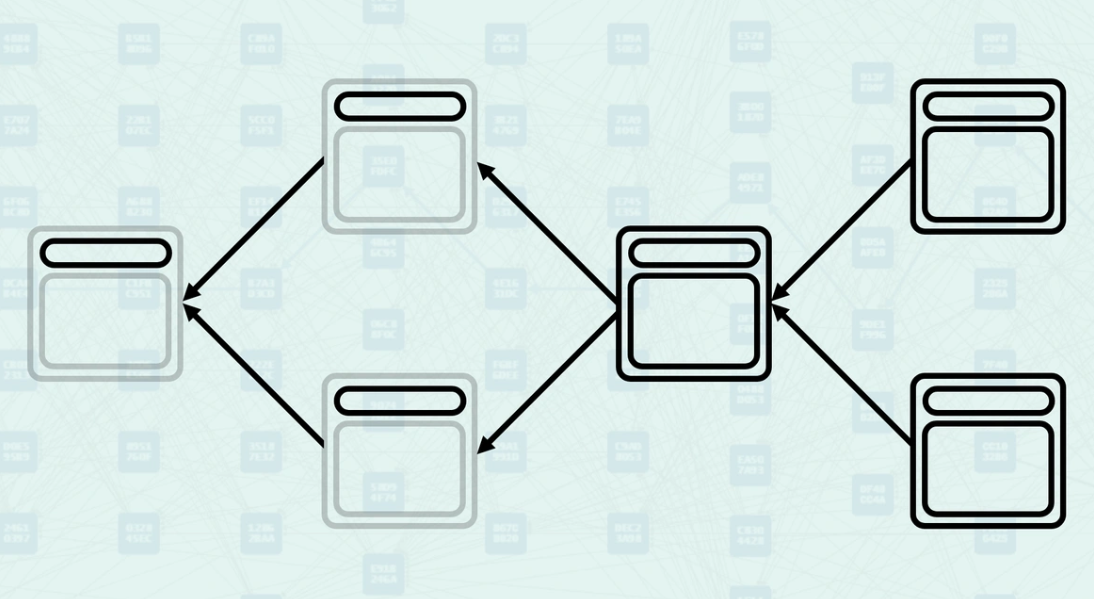
Selected Parent Selection - Among all parents, the system selects one as the "selected parent" - the one with the greatest "blue work". This creates a main chain backbone through the DAG while acknowledging other parental relationships. Here, the parental chain is highlighted.
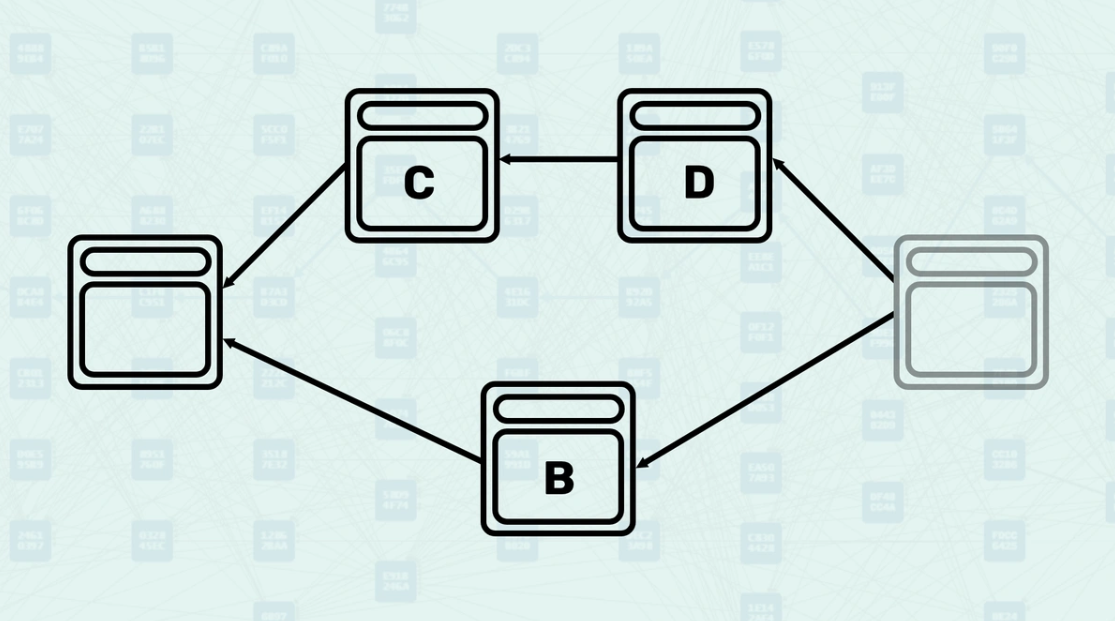
Mergeset Processing - Once the selected parent is chosen, the mergeset is calculated and processed to determine the final GHOSTDAG data. The mergeset excludes the selected parent since it is already accounted for in the main chain. Here, the mergeset includes block C, as it is in the anticone of block B (the selected parent) even though it is not a parent of the new block (parents only include block B and block D).
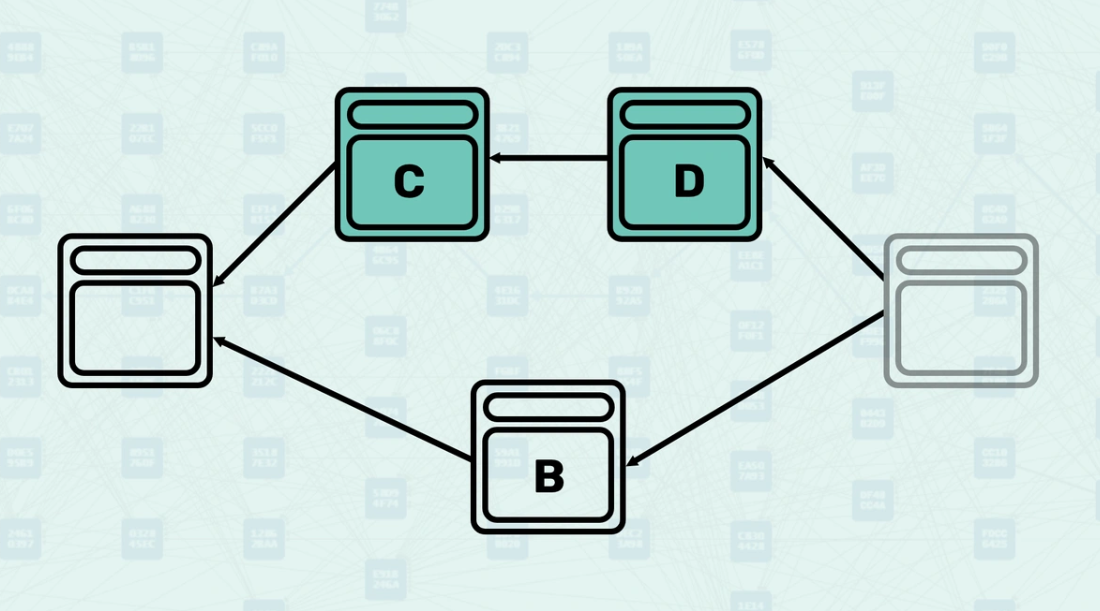
Virtual Parent Selection - When creating the virtual state, the system uses both concepts: it chooses virtual parents from candidate blocks while ensuring that the resulting mergeset does not exceed size limits. This balances the inclusion of many parallel blocks while maintaining manageable consensus complexity.
Practical Differences
Storage and Iteration - Parents are stored directly in block headers, while mergeset data is calculated and stored separately in GHOSTDAG data structures. The system provides different iterators to access mergeset blocks in various orders (consensus order, "blue work" order, etc.).
Impact on Consensus - Parents determine the basic structure of the DAG, but the mergeset determines which blocks actually contribute to consensus calculations like "blue score" and "blue work". A block could be a parent but end up being colored red in the mergeset, meaning it does not contribute to the main consensus chain.
Simplified Definitions
Parents - The blocks that a new block directly references in its header, establishing explicit relationships in the DAG.
Mergeset - The set of blocks in a block's anticone that are considered for consensus processing, excluding the selected parent.
Selected Parent - The parent with the greatest "blue work", forming the backbone of the main chain.
Blue/Red Mergeset - Blocks in the mergeset that contribute to consensus (blue) or not (red).
Parents define the DAG structure, while the mergeset determines participation in consensus.
Bitcoin vs Kaspa
Bitcoin - Has only one parent per block (except Genesis), so there is no distinction between parents and mergeset. The single parent is both the structural and consensus relationship.
Kaspa - Separates structural relationships (parents) from consensus relationships (mergeset). Multiple parents create the DAG structure, but mergeset processing determines which blocks actually contribute to the consensus state.
Chapter 7: Second Order Pruning
What is second order pruning and how does Kaspa use it?
Second order pruning is the advanced step in Kaspa's storage optimization that removes consensus-related data while maintaining the ability to validate new blocks and participate in network consensus. It goes beyond first order pruning by selectively removing DAG structure data, relationships, and some headers themselves.
Why "Second Order"? - This terminology emphasizes that after block bodies are removed (First Order), Kaspa can remove additional consensus data while retaining validation capabilities. Second order pruning allows for maximum storage efficiency by removing redundant consensus information that is not essential for continuous validation.
What does that mean? - This article assumes knowledge of first order pruning, so we will start with the consensus data that exists after first order pruning, then explain how second order pruning selectively removes consensus structures, what is retained versus what is removed, and how validation continues to function with reduced consensus data.
First Order Pruning vs Second Order Pruning
Foundation of First Order Pruning - After first order pruning, nodes retain all block headers, GHOSTDAG data, accessibility relationships, and DAG structure information. This allows for full consensus validation but still requires significant storage for the complex DAG relationships that Kaspa maintains.
Challenge of Second Order Pruning - The challenge is to determine which consensus data can be safely removed without compromising the node's ability to validate new blocks. The system must preserve enough structural information to maintain consensus while removing redundant data.
Multi-Level Proof System
Proof Level Classification - Kaspa's pruning system classifies blocks based on their importance for different proof levels. Blocks affiliated with higher proof levels retain more consensus data than those only needed for lower levels.
Level-Based Data Retention - The system determines which consensus data to retain based on the proof level each block belongs to. Higher-level blocks retain more relationships and consensus information, while lower-level blocks can have their consensus data safely removed.
Contiguous DAG Zones - Pruning ensures that for each level, the remaining relationships represent a contiguous DAG zone, maintaining the structural integrity necessary for consensus validation.
What is removed in Second Order Pruning
Removal of Relationship Data - Second order pruning removes level-specific relationship data for blocks that only belong to higher proof levels. This preserves the semantics that relationships represent contiguous DAG zones while removing unnecessary lower-level data.
Selective Removal of GHOSTDAG Data - The system removes GHOSTDAG data for certain blocks while preserving it for essential consensus validation. GHOSTDAG data is removed at level 0 for partially pruned blocks.
Removal of Headers - In the most aggressive form of second order pruning, some block headers themselves can be removed while preserving past pruning points. Only non-essential headers for pruning point queries are removed.
What is retained in Second Order Pruning
Essential Consensus Structures - Critical consensus data such as the anticone of the pruning point, DAA window blocks, and GHOSTDAG blocks for essential validation are always retained. This ensures that consensus operations can continue even with reduced data storage.
Proof Level Affiliations - Blocks maintain their classification based on proof level importance, determining which data is retained. The system preserves the minimum data necessary for consensus validation based on these affiliations.
Past Pruning Points - Headers for past pruning points are always retained to maintain the ability to respond to pruning point queries and support the pruning proof system.
How Consensus Validation Continues
Status Transitions - Blocks undergoing second order pruning transition to "header-only" status when they had a valid status and belong to a proof level. This preserves the semantics that a valid status implies the existence of essential consensus data.
Validation of Reduced Data - Even with second order pruning, nodes can validate new blocks using the preserved consensus data structures and remaining relationships. The system maintains enough information to verify GHOSTDAG rules and relationships between blocks.
Proof-Based Validation - Preserved proof level data allows nodes to validate blocks using cryptographic proofs rather than full historical consensus data, enabling participation in consensus with significantly reduced storage.
Archive Nodes vs Pruning Nodes
Archive Node Behavior - Nodes configured as archive entirely ignore first and second order pruning, preserving all consensus data. These nodes serve as a complete consensus ledger of the network but require maximum storage.
Pruning Node Efficiency - Regular pruning nodes use second order pruning to achieve maximum storage efficiency while maintaining full consensus validation capabilities through the multi-level proof system.
Note: For a detailed explanation of how pruning nodes remain full nodes and why archive nodes are optional for network operation (maintaining Bitcoin's trustless model), see the extended article "Archive Node vs Full Node" which covers validation capabilities, cryptographic proofs, and network sustainability.
Simplified Definitions
Second Order Pruning - Removal of consensus-related data while preserving enough information to validate consensus rules.
Proof Level Affiliation - Classification of blocks based on the proof levels they belong to, determining which consensus data is retained.
"Header-Only" Status - Blocks whose consensus data has been pruned but retain essential validation information.
Contiguous DAG Zones - Maintaining structural integrity in the remaining consensus data after pruning.
Second order pruning allows for maximum storage efficiency while preserving consensus validation capabilities through intelligent data classification.
Bitcoin vs Kaspa: Pruning Consensus Data
Bitcoin - Consensus information is essential for validation and cannot be safely removed.
Kaspa - The complex DAG structure and multi-level proof system allow for sophisticated second order pruning where different levels of consensus data can be selectively removed based on their importance for validation. This allows for much more aggressive storage optimization while maintaining consensus capabilities.
Chapter 8: Kaspa GHOSTDAG Simplified
What is GHOSTDAG and how does Kaspa use it?
A consensus protocol that orders blocks in a DAG structure while maintaining security properties.
What does that mean? This article explains GHOSTDAG by starting with traditional consensus, then GHOSTDAG's approach, how it classifies blocks, and how it differs between Bitcoin and Kaspa.
Traditional Consensus - Linear Chain Order
Traditional blockchain consensus operates on a linear chain where blocks form a single sequence. Each block has exactly one parent (except Genesis), creating a simple ordering mechanism. When conflicts arise (multiple blocks at the same height), the network selects one block and rejects the others as orphans. This approach ensures clear ordering but limits throughput as only one block can be accepted at each level.
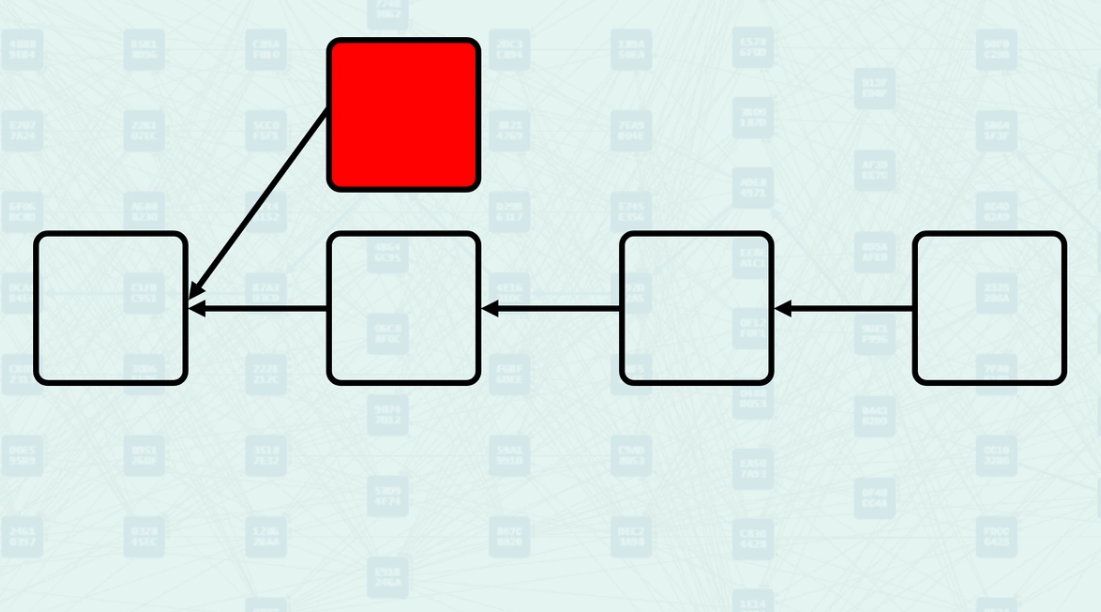
GHOSTDAG Protocol - DAG Consensus
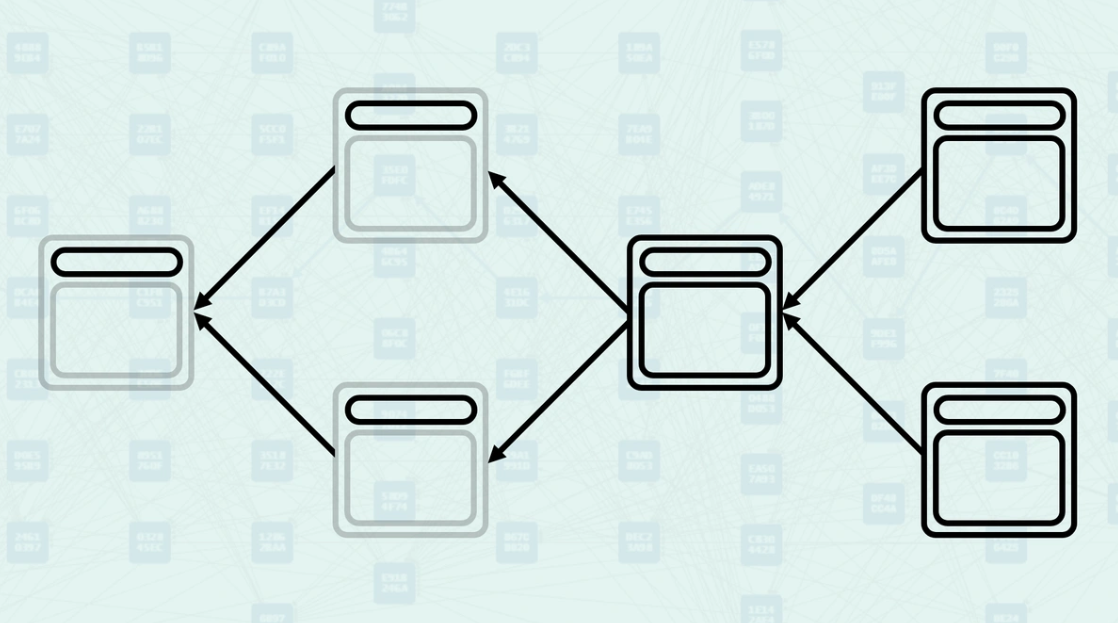
GHOSTDAG extends consensus to work with Directed Acyclic Graph (DAG) structures where blocks can have multiple parents. The protocol processes blocks by first selecting a parent with the highest "Blue Work," then examining all blocks in the Mergeset to classify them as "blue" (honest) or "red" (potentially conflicting). This classification is based on mathematical constraints involving the security parameter K, which limits the size of Anticones to maintain security properties.
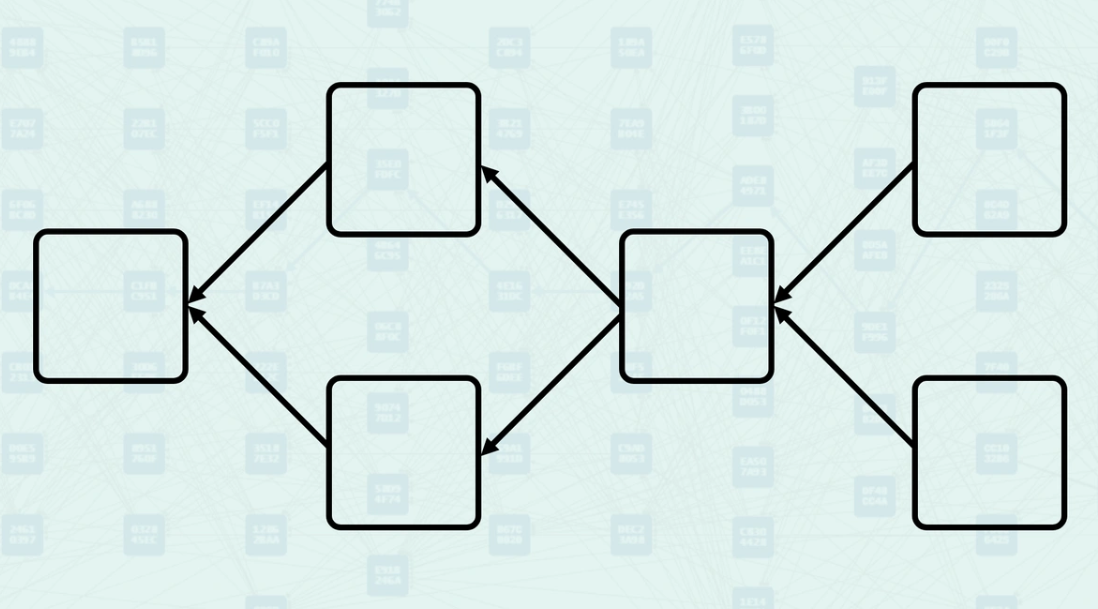
Block Classification Rules
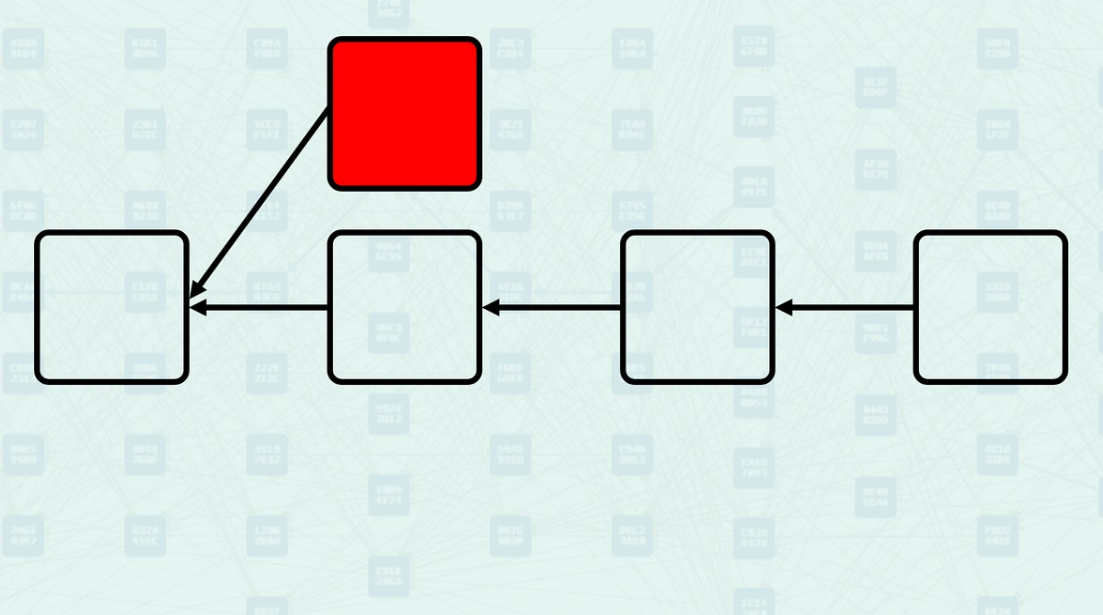
GHOSTDAG classifies blocks using two key constraints related to the security parameter K. First, the number of blue blocks in a candidate block's Anticone must not exceed K blocks. Second, for each existing blue block, adding the candidate must not cause any blue block's Anticone to exceed K blocks. The algorithm keeps track of Anticone size to efficiently validate these constraints during block processing. The gray block here is currently being validated by the network, block C is its Selected Parent. If k=0, then chain block C is already 1 blue block, causing block B to be classified as Red. If k = 1 (or more), block B is classified as blue, as it only has 1 blue block (block C) in its Anticone.
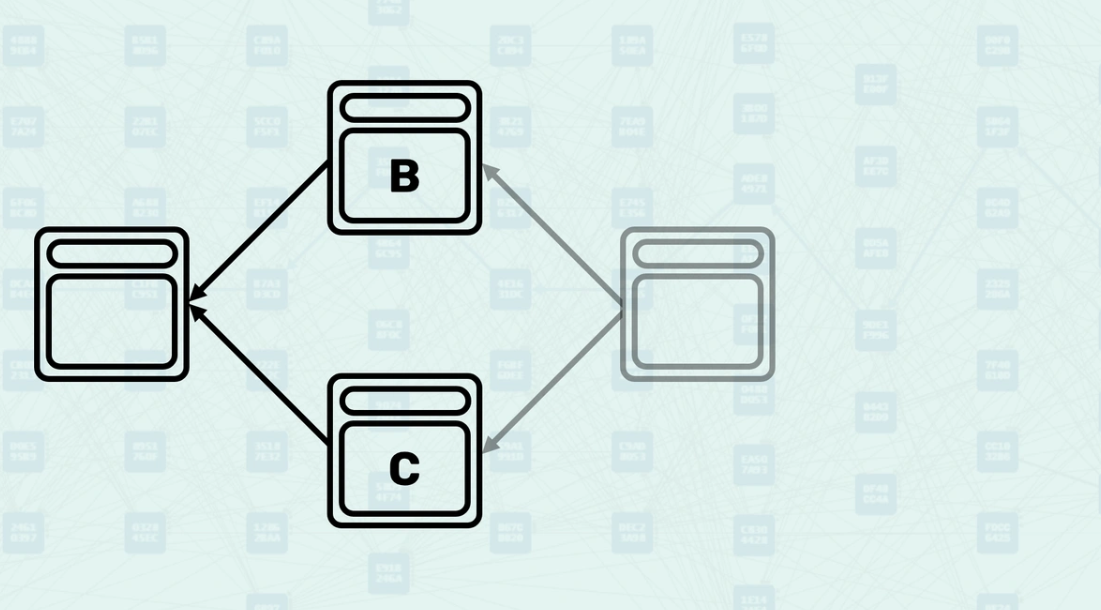
Blue Work Accumulation
The protocol accumulates proof-of-work only from blue blocks, creating the "Blue Work" metric. Blue blocks contribute their computational work to the cumulative security score, while red blocks are excluded from this calculation. This selective accumulation ensures that only consensus-valid blocks contribute to network security, preventing malicious or conflicting blocks from undermining the system. In this example, assuming block B is red (k=0), the "Blue Work" of our gray block would be calculated as the "Blue Work" inherited from block C, plus the "Blue Work" of block C. If block B is blue, the "Blue Work" of our new block would inherit the "Blue Work" of its Selected Parent (block C), then add the "Blue Work" of its Selected Parent (C) and the "Blue Work" of the blue blocks in its Mergeset (block B).
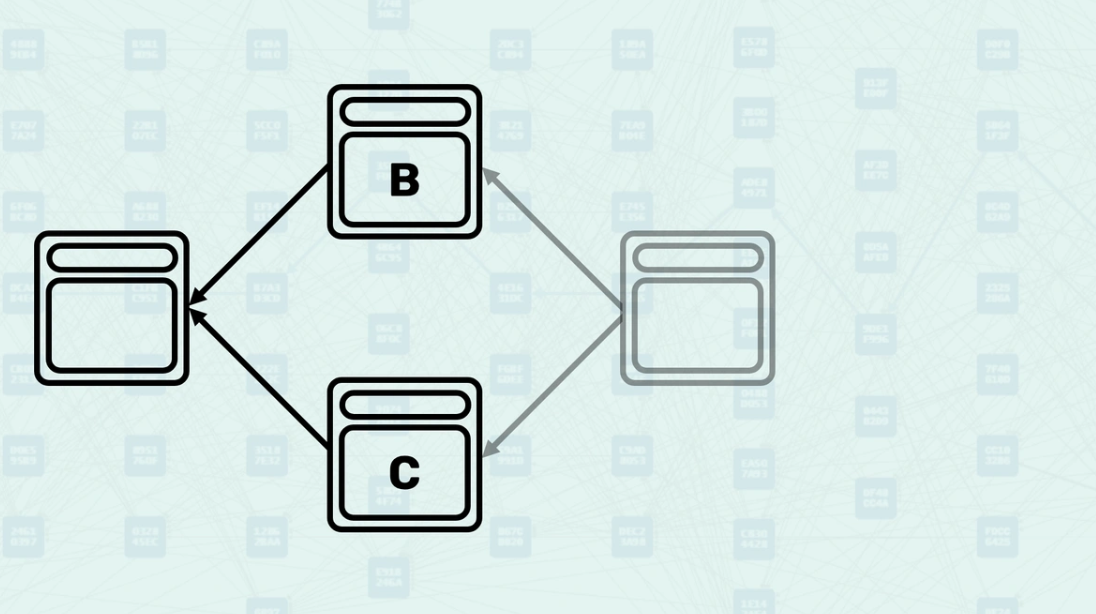
Parent Selection and Ordering
GHOSTDAG determines block ordering by parent selection based on "Blue Work" values. The protocol selects the parent with the highest accumulated "Blue Work" as the "Selected Parent," creating a backbone chain within the DAG structure. Block ordering uses "Blue Work" as the primary criterion, with block header hash providing deterministic ordering in case of ties. In our example, we assume block C is the Selected Parent and block B is blue. The ordering for transaction processing is 1. Selected Parent (C) 2. Ordered Mergeset (B)
Data Storage and Management
The protocol stores classification results in structured data containing lists of blue and red blocks. Blue blocks are added with Anticone size tracking for future classification decisions, while red blocks are simply added to the red list. This organization maintains complete DAG information while clearly distinguishing consensus roles.
Simplified Definitions
Traditional Consensus - A linear chain ordering system where blocks form a single sequence with one parent per block.
GHOSTDAG Protocol - A DAG consensus mechanism that classifies blocks as blue or red based on Anticone size constraints.
Block Classification - The process of determining whether blocks are blue (consensus-valid) or red (potentially conflicting).
Blue Work Accumulation - A selective counting of proof-of-work that only includes work from blue blocks.
GHOSTDAG is a consensus protocol that enables DAG structures while maintaining blockchain security properties.
Bitcoin and Kaspa
Bitcoin - Uses traditional linear chain consensus where blocks form a single sequence. Conflicting blocks are orphaned and contribute no security. The longest chain (most accumulated work) determines consensus through a simple comparison mechanism.
Kaspa - Uses the GHOSTDAG protocol to manage DAG structures with multiple concurrent blocks. Blue blocks contribute to security through "Blue Work" accumulation, while red blocks remain in the DAG but are excluded from consensus decisions. The protocol maintains both types of blocks for comprehensive network state tracking.
Chapter 9: DAG Terminology
Past, Future, Anticone, Mergeset, K parameter, what does it all mean?
Past, Future, and Anticone are DAG terms, while Mergeset and K are used in GHOSTDAG.
DAG terminology is a specialized vocabulary for describing relationships in a BlockDAG structure. We will start with the linear chain, the DAG, then a touch of GHOSTDAG.
Linear Chain Terminology - Traditional Blockchain
Linear chain terminology uses simple concepts where blocks form a single sequence. Each block has a parent and potentially a child, creating simple ancestor-descendant relationships. Terms like "height," "previous block," and "next block" describe the linear progression. When conflicts arise, blocks are either "accepted" into the main chain or "orphaned" and discarded.
DAG Terminology
Allowing blocks to have multiple parents creates new relationships within the DAG.
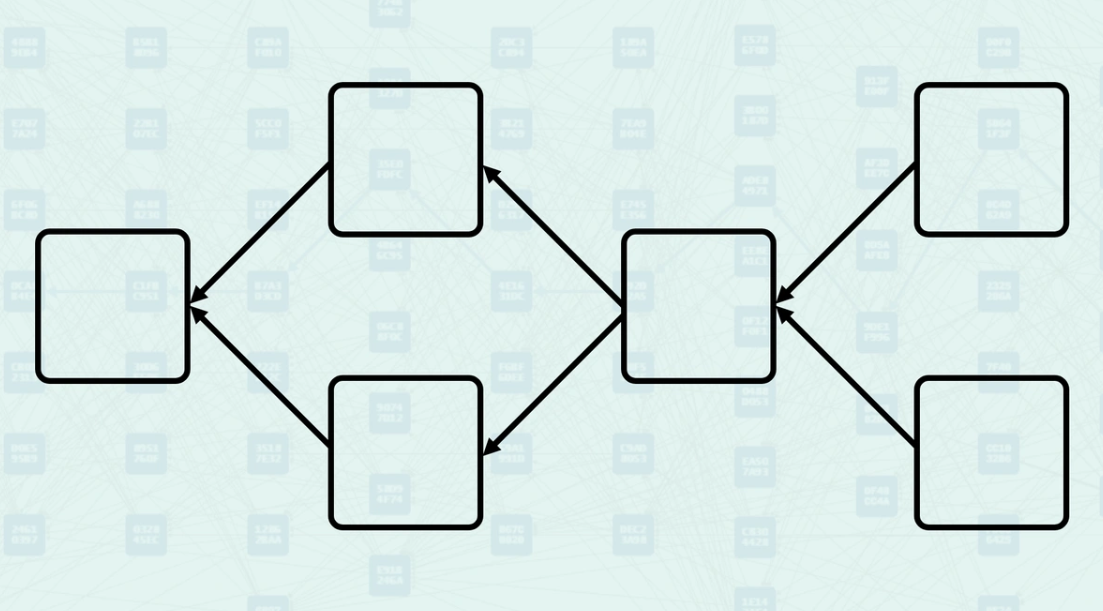
Past and Future Relationships - DAG
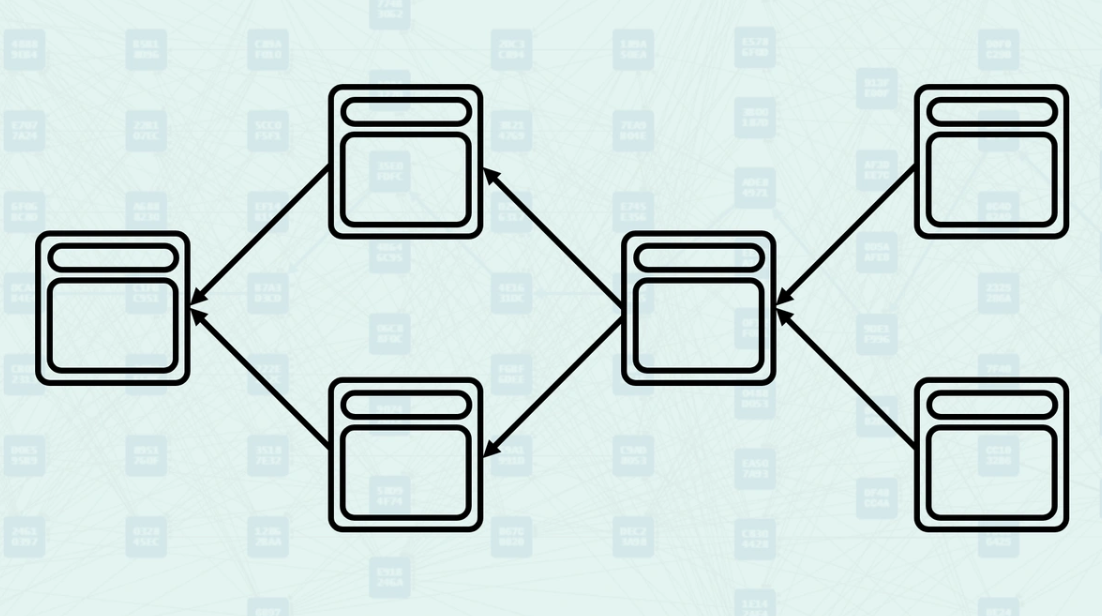
The Past relationship defines all blocks reachable by following parent links backward from a given block. A block is in another's past if there is a directed path connecting them. The Future relationship works inversely - if block A is in block B's past, then B is in A's future.
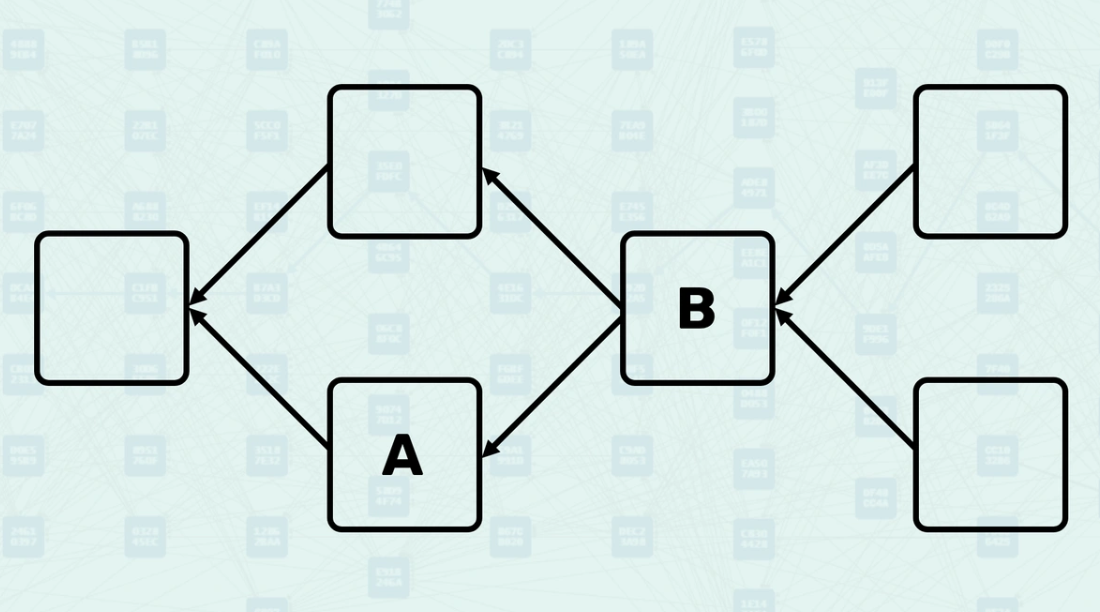
Anticone Relationship - DAG
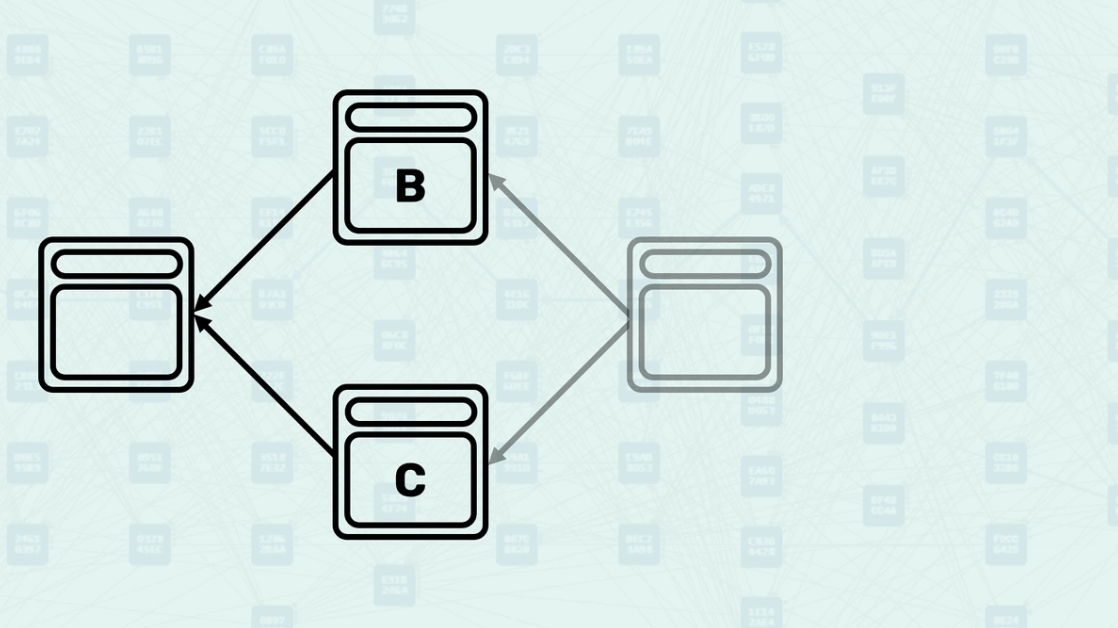
The Anticone describes blocks that are neither ancestors nor descendants of each other - they exist concurrently in the DAG. Two blocks are in each other's Anticone if neither can reach the other via a directed path. This relationship is crucial for GHOSTDAG's security parameter K, which limits the size of Anticones to maintain consensus security. Here, block B and block C are in each other's Anticone, block B is not reachable from block C, and block C is not reachable from block B.
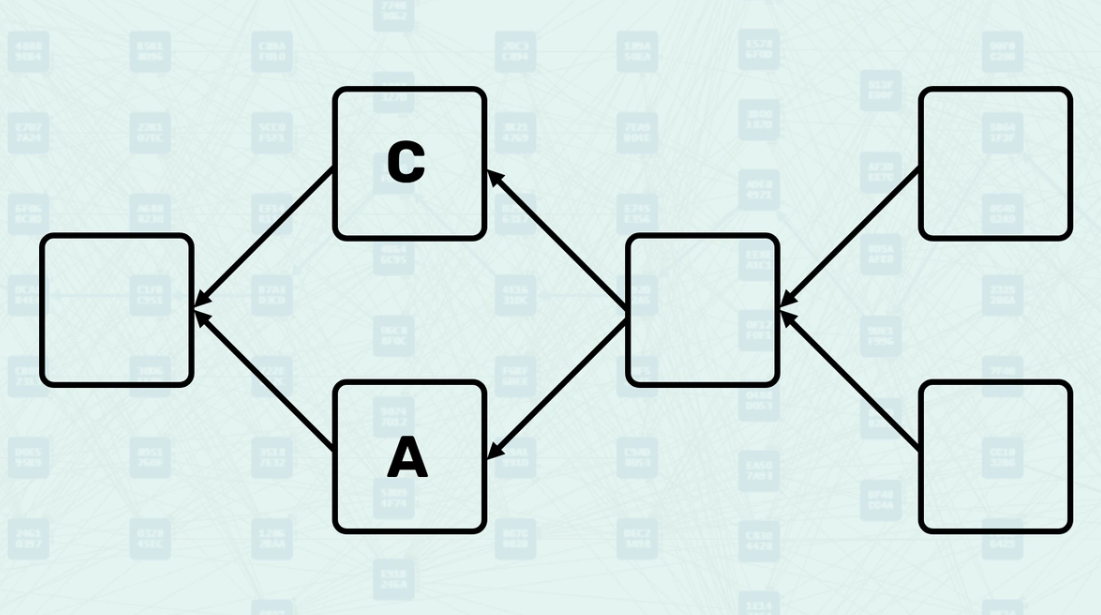
Mergeset and Blue/Red Classification - GHOSTDAG
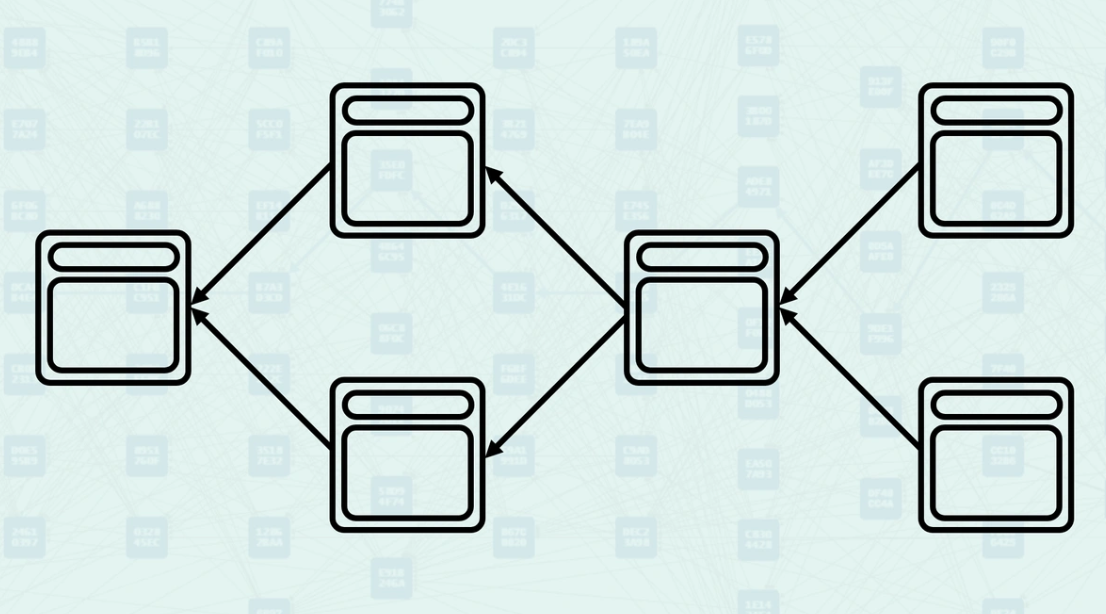
The Mergeset refers to the collection of blocks that are merged when a new block is created. The Mergeset contains a block's direct parents, but can also contain blocks that are not direct parents. GHOSTDAG classifies blocks in the Mergeset as "Blue" (honest) or "Red" (potentially conflicting) based on Anticone size constraints. This classification determines which blocks contribute to network security through "Blue Work" accumulation. Here is an example of block B classifying its Mergeset as Blue and Red when the Anticone size constraint = 0.
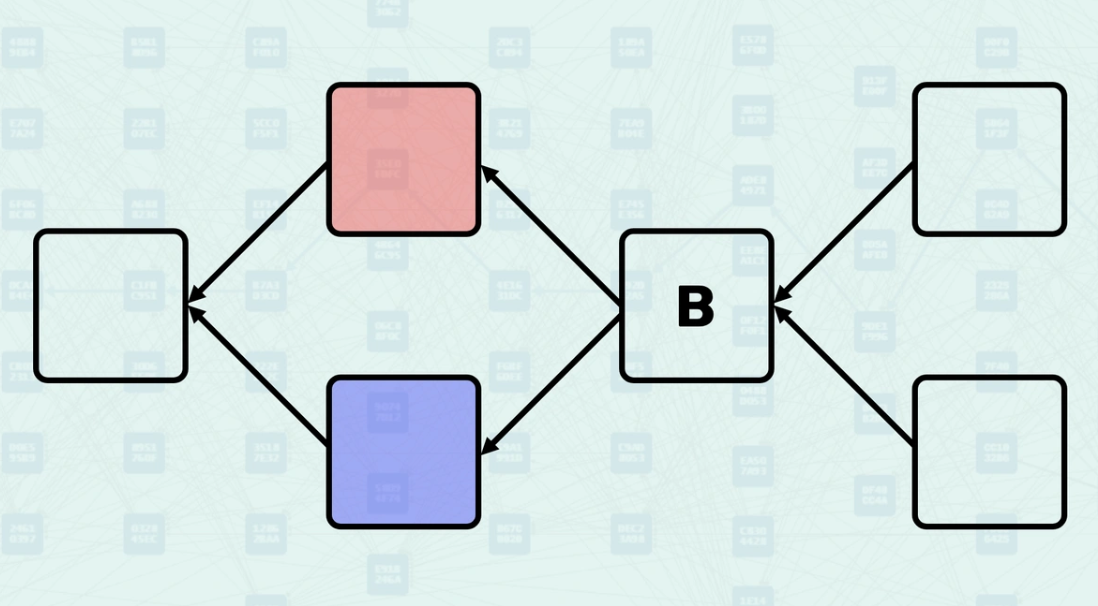
K Parameter - GHOSTDAG
The K parameter controls the maximum allowed size of the Anticone for blue blocks. This parameter is calculated based on network latency, block production rate, and desired security guarantees. In this example, instead of k = 0 as in the example above, k = 1, so each blue block has 1 other blue block in its Anticone.
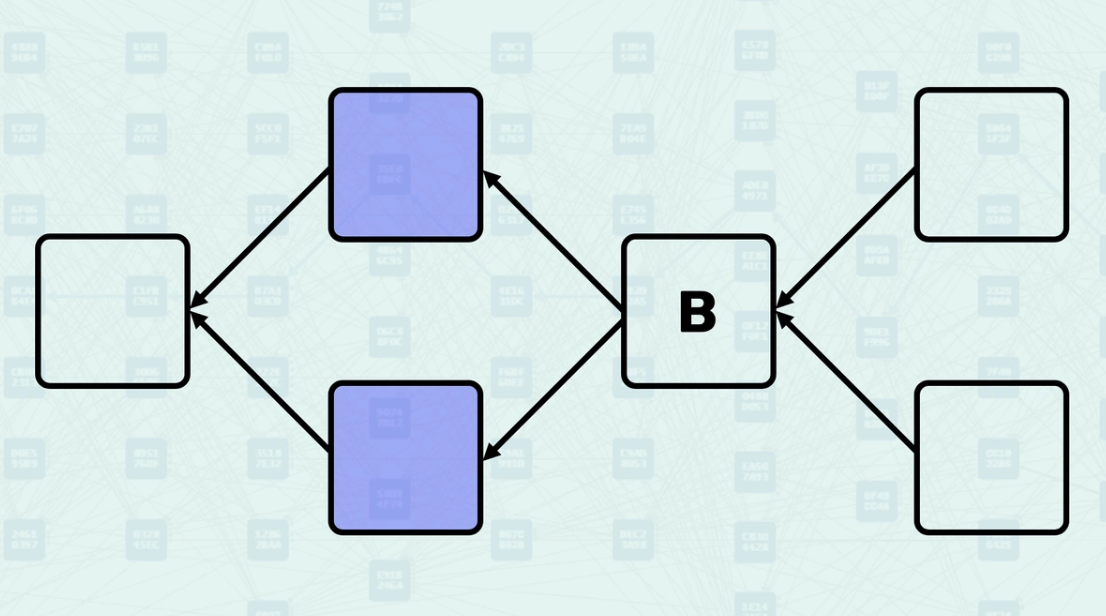
Simplified Definitions
Past Relationship - All blocks reachable by following parent links backward from a given block.
Future Relationship - All blocks that can reach a given block by following parent links forward.
Anticone Relationship - Blocks that are neither ancestors nor descendants of each other.
Mergeset - Collection of GHOSTDAG blocks merged when a new block is created.
Blue/Red Classification - Categorization of blocks by GHOSTDAG as honest (blue) or potentially conflicting (red).
Security Parameter K - Maximum allowed size of GHOSTDAG's anticone to maintain consensus security.
Bitcoin and Kaspa
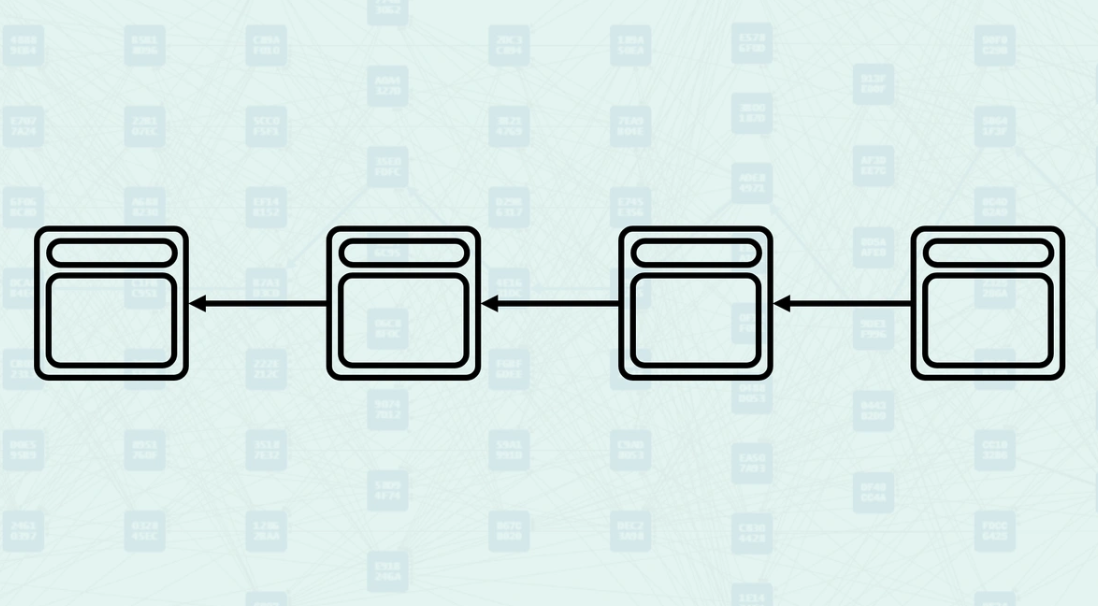
Bitcoin - Uses simple linear terminology: "previous block," "next block," "chain height," and "longest chain." Relationships are simple ancestor-descendant connections. Competing blocks are "orphaned" with no intermediate states.
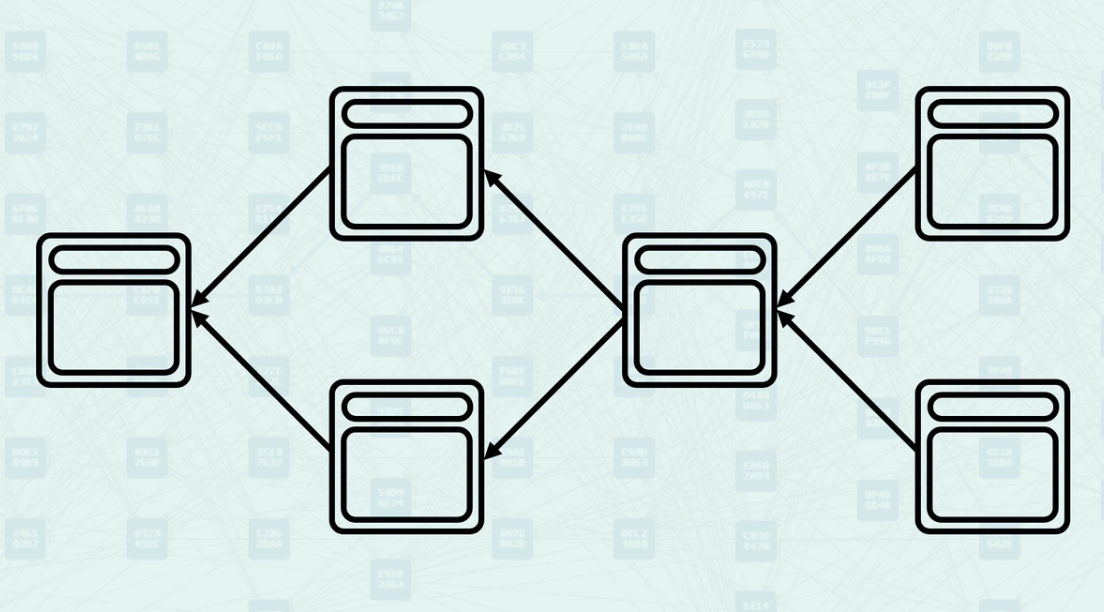
Kaspa - Uses additional terminology, including DAG's Past/Future/Anticone relationships, GHOSTDAG's Mergeset, and Mergeset's Blue/Red classification. Kaspa maintains multiple concurrent blocks, manages their relationships, and provides consistent ordering.
Chapter 10: First Order Pruning
What is first order pruning and how does Kaspa use it?
First order pruning is the first step in Kaspa's multi-phase storage optimization. It removes old transaction data from blocks while maintaining a UTXO set at the pruning point for state validation - but crucially, it preserves all block headers to maintain blockchain integrity.
Why "First Order"? - This terminology emphasizes that removing block bodies is just the beginning. While first order pruning significantly reduces storage requirements and lowers the barriers to running a node (increasing decentralization), it is followed by additional pruning steps that can remove even more data (second order pruning). This article specifically focuses on block body removal - the foundation that makes all subsequent optimizations possible.
What does that mean? - This article assumes no prior knowledge, so we will start with traditional blockchain storage challenges, then explain how first order pruning works by maintaining UTXO sets, what is removed versus what is preserved, how the pruning point UTXO set enables validation, and how this creates the foundation for Kaspa's scalable storage model that allows for broader network participation.
Traditional Storage vs First Order Pruning
Traditional Full Storage - In traditional blockchain implementations, nodes store full block data, including all transaction details from Genesis to the current tip. This means that every input, output, signature, and transaction script is preserved forever, leading to ever-increasing storage requirements that can become prohibitive for many users.
Challenge of First Order Pruning - The challenge is to remove old transaction data while still being able to validate new transactions. New transactions must reference previous outputs (UTXOs), so the system must maintain enough information to validate these references even after old block bodies are pruned.
The UTXO set as a foundation
Definition of the UTXO set - The UTXO set represents all unspent transaction outputs at a specific point in the blockchain. A snapshot of all "coins" that exist and can be spent at that moment, similar to an inventory of all money in circulation.
Pruning Point UTXO Set - Kaspa maintains a special UTXO set at the Pruning Point, which serves as the base state for validation. This UTXO set is updated as the Pruning Point advances, ensuring that it always reflects the correct spendable state at that checkpoint.
Advancement of the UTXO Set - When the Pruning Point advances, the system applies the UTXO differences from blocks in the chain to update the pruning point UTXO set. This process ensures that the UTXO set remains accurate as old data is pruned.
What is pruned in First Order Pruning
Removal of Block Body Data - First order pruning removes the actual transaction data from old blocks, including transaction inputs, outputs, signatures, and scripts. This includes UTXO multisets, UTXO differences, acceptance data, and the full block transaction store.
Header Preservation - Although transaction data is removed, block headers are preserved to maintain the structural integrity of the blockchain. Blocks transition to "header-only" status, indicating that the header exists but the body has been pruned.
Retention of Essential Data - The system preserves critical data necessary for consensus validation, including the anticone of the pruning point, DAA window blocks, and GHOSTDAG blocks. This ensures that consensus operations can continue even after pruning.
How the UTXO set enables validation
Transaction Validation Process - New transactions can be validated against the pruning point UTXO set plus all subsequent UTXO changes. The system validates that the referenced UTXOs exist and have not been double-spent, even without the original transaction data.
State Reconstruction - The UTXO set at the pruning point, combined with UTXO differences from subsequent blocks, allows for the reconstruction of the current spendable state. This enables full validation capabilities without requiring full historical transaction data.
Commitment Verification - The system can verify the integrity of the UTXO set using cryptographic commitments in block headers. This ensures that the pruned UTXO set matches what the blockchain headers claim it should be.
Archive Nodes vs Pruning Nodes
Archive Node Behavior - Nodes configured as archive entirely ignore first order pruning, preserving all transaction data. These nodes serve as a complete historical ledger of the network but require significantly more storage.
Pruning Node Efficiency - Regular pruning nodes use first order pruning to maintain manageable storage while fully participating in consensus validation. The UTXO set provides enough information to validate new transactions without requiring full historical data.
Addressing concerns about pruning and genesis proof
A recurring concern is that gaps in the ledger history due to pruning could compromise the verifiability of the chain from its inception (the genesis block), and particularly the proof that there was no pre-mining.
This concern is unfounded. Here's why:
- The genesis block is built into the code: The genesis block itself is "hardcoded" into the Kaspa node software. This genesis block contains an empty UTXO set, which proves that there was no pre-mining. Any user can verify this in the public source code.
- The genesis proof: Each node maintains a "genesis proof." This is a short chain of data that cryptographically proves that the current state of the ledger has indeed evolved from the embedded genesis block. Forging such a proof would require as much work as was invested to create the entire ledger. In other words, this proof is as strong as owning the complete history.
- The integrity of the reconstructed history: Although efforts are made to reconstruct the complete history for research and convenience purposes, the process is decentralized. Data is collected from many users. No single actor has control over the remaining "gaps," making it impossible to selectively "hide" a part of the history.
In summary, Kaspa's pruning mechanism is designed so that the network remains safe, secure, and transparent, even without any archive nodes. The verifiability of the chain from its genesis is guaranteed by robust cryptographic proofs, and not by the need to store a complete and increasingly heavy history.
Simplified Definitions
First Order Pruning - Removal of old block transaction data while maintaining a UTXO set for validation.
Pruning Point UTXO Set - A snapshot of all spendable outputs at the pruning point, used as the basis for validation.
"Header-Only" Status - Blocks whose transaction data has been pruned but retain their headers.
UTXO Advancement - The process of updating the pruning point UTXO set as the pruning point advances.
First order pruning enables storage efficiency while preserving validation capabilities through UTXO sets.
Bitcoin vs Kaspa: Full Node Bootstrapping
Bitcoin - Full nodes must download and validate all block data from genesis to bootstrap, requiring full historical transaction data. While Bitcoin supports simple pruning after initial synchronization, new nodes still need the full blockchain history to establish the initial state. The linear chain structure makes this process straightforward but storage-intensive.
Kaspa - Full nodes can bootstrap using pruning proofs without downloading full historical data, thanks to the integration of first order pruning with the consensus protocol. The system validates pruning proofs and applies cryptographically verifiable data ("trustworthy data") to establish the initial state. This "trustworthy data" requires no trust in any party - it is mathematically verified by cryptographic proofs that guarantee the data conforms to consensus rules. The validation process cryptographically proves that the pruning point proof represents a valid consensus state, while trustworthy data undergoes rigorous verification to ensure it matches the expected state of the blockchain. This allows new nodes to synchronize efficiently while maintaining full validation capabilities without trusting an external party.
Chapter 11: Archive Nodes vs Full Nodes
Kaspa Archive Nodes vs Pruning Nodes
Pruning Nodes Are Full Nodes - Pruning nodes that use first order pruning and second order pruning are still considered Full Nodes because they maintain full validation capabilities. They can validate all new blocks, participate in consensus, and serve the network without requiring trust in external parties. The pruning point proof system ensures that even with pruned data, these nodes maintain cryptographic verification of the full blockchain state.
Archive Nodes Are Optional - Archive nodes that retain all historical data are not necessary for the Kaspa network to operate indefinitely. The network can operate entirely with pruning nodes because pruning point proofs provide mathematically verifiable guarantees about the pruned state. This is in contrast to Bitcoin, where the network requires Archive Nodes (which store the full transaction history from genesis) to bootstrap a new node.
No Additional Trust Requirement - The pruning system maintains Bitcoin's trustless model by using cryptographic proofs rather than trusted parties. New nodes can bootstrap from pruning proofs and verify the full blockchain state without downloading the entire historical data, while maintaining the same security guarantees as nodes that store everything from Genesis.
Network Sustainability - This design ensures that the Kaspa network can scale sustainably without requiring ever-increasing storage from participants. Pruning nodes offer the same consensus security as archive nodes while allowing broader network participation through reduced hardware requirements.
Archive Node Behavior - Nodes configured as archive entirely ignore first order pruning and second order pruning, preserving all consensus data (and historical application data). These nodes serve as a complete consensus ledger of the network but require maximum storage and are purely optional for network operation.
Pruning Node Efficiency - Regular pruning nodes (Full Nodes) use pruning to achieve maximum storage efficiency while maintaining full consensus validation capabilities through the multi-level proof system. These nodes are indistinguishable from archive nodes in terms of security and validation capabilities.
Chapter 12: Kaspa: An Evolution in Energy-Efficient Decentralized Architecture
Introduction: The Physics of Money and Efficiency
In the world of decentralized networks, efficiency is not just a luxury, it's a survival trait. Cryptocurrencies function as monetary energy systems, where real-world energy is converted into secure, immutable records of value. Just as physical systems strive to minimize wasted energy and entropy, a well-designed crypto network should minimize waste and friction. Bitcoin pioneered this concept by linking monetary value to the energy expenditure of proof-of-work, creating a form of "digital gold" secured by thermodynamic cost. But Bitcoin's architecture, while revolutionary, has structural inefficiencies that limit its throughput and waste some of the energy miners put into it.
Enter Kaspa - a next-generation proof-of-work network that redefines the architecture of decentralized consensus. Kaspa is built on a blockDAG (Directed Acyclic Graph) rather than a single chain, allowing multiple blocks to be created and processed in parallel. This design aims to minimize system entropy and inefficiency, making Kaspa a kind of "efficient engine" for storing and moving economic value.
Entropy, Energy, and Monetary Systems
To understand Kaspa's significance, we must first grasp how energy and entropy relate to monetary systems. In physics, creating order (low entropy) in one place requires expending energy and increasing entropy elsewhere - a principle that also applies to money. Hard money like gold historically derived its value from the immense energy and labor required to obtain it. Bitcoin applied this same principle digitally, requiring miners to perform costly computations (hashing) to add blocks, thereby ensuring that each coin and block bears proof of expended energy. However, if a significant portion of the work is wasted or if the system design causes unnecessary friction, then the "monetary engine" loses energy as heat.
Friction in Economic Systems
In economics, friction refers to anything that causes loss or inefficiency in the movement of value. Bitcoin introduced some friction out of necessity: its design trades speed for security. Transactions wait about 10 minutes on average for a new block, and the convention is to wait 6 confirmations (about 1 hour) for high assurance against reversal. This latency and low throughput create economic friction. Furthermore, Bitcoin's mining process sometimes produces wasted work in the form of orphaned blocks (when two miners find a valid block almost at the same time, only one block becomes part of the main chain and the other is discarded). These orphaned blocks represent real energy expended by miners that does not contribute sustainably to the ledger.
Bitcoin's Single-Chain Bottleneck
The Bitcoin blockchain can be visualized as a single-lane road for transactions. Only one block can be accepted at a time, and each block must align sequentially. If two blocks arrive at the same time, one will be forced to yield and will effectively be discarded as an orphan. This design was chosen deliberately to keep the system in order, but at the cost of severe performance limitations. The limitations of this single-chain architecture are well-known: lack of scalability, susceptibility to selfish mining attacks if block times were reduced, and wasted blocks are inherent problems. Critically, Bitcoin's consensus wastes a small but non-negligible portion of mining work on blocks that never become part of the ledger. These orphaned blocks are the system's entropy - energy that increased disorder and was dissipated as heat, not stored as useful information. The result is that Bitcoin's enormous mining energy produces only a trickle of throughput.
Kaspa's BlockDAG: Parallelism without Wasted Work
Kaspa approached the problem by asking: what if blocks didn't have to line up single file? Instead of a single-lane road, Kaspa uses a multi-lane highway for blocks, where many blocks can be created in parallel and still merge into a single ledger. The fundamental innovation is Kaspa's blockDAG (Directed Acyclic Graph) architecture combined with the GHOSTDAG consensus protocol. In a blockDAG, blocks do not point to a single previous block (the tip of the "longest chain") as in Bitcoin; instead, each block can reference multiple predecessors, including different "tips" of the graph. Blocks that would be considered competing or orphaned in Bitcoin are not discarded in Kaspa - they are incorporated into the ledger graph. The DAG structure allows these simultaneous blocks to coexist and eventually be ordered consistently by the GhostDAG algorithm. All valid blocks contribute to the ledger history; no miner's proof-of-work is wasted.
The impact of this design on efficiency is spectacular. First, no mining power is wasted on orphaned blocks. Second, Kaspa's parallelism significantly increases throughput. Kaspa operates at a base rate of 1 block per second on its mainnet (and has recently been upgraded to 10 blocks per second), compared to 0.1 blocks per second for Bitcoin. This is a 10-fold increase in block frequency by design, with plans for even more. Furthermore, because each Kaspa block is smaller (to keep node requirements low) but they arrive much more frequently, transactions are spread across many blocks. The end result is a potential throughput of thousands of transactions per second. In fact, the GhostDAG algorithm has demonstrated that it can support approximately 3000 transactions per second with 10 blocks/sec on test networks using common hardware. This has been achieved while maintaining modest hardware requirements. In other words, Kaspa's architecture does not force a trade-off between scalability and decentralization - it processes many more transactions without increasing the barrier to entry for nodes. Every participant can still validate the chain on ordinary computers, which is crucial for decentralization. Unlike many high-throughput systems that rely on powerful data center nodes or compromise consensus, Kaspa remains a pure proof-of-work system with a wide distribution of mining and full nodes.
How does Kaspa maintain a unique and agreed-upon history (a single source of truth) if blocks arrive in parallel? The answer is GhostDAG, a consensus algorithm that orders blocks in the DAG by considering not only the "longest chain" (as in Bitcoin) but the "heaviest subgraph" of blocks. GhostDAG assigns each block a kind of score or ordering based on the amount of validated history preceding it and how it references other blocks. It finds a pattern called a k-cluster - essentially a set of mutually aware blocks - and uses it to decide which blocks are part of the main ordered structure (colored "blue") and which are outside the main structure ("red") but still included. The algorithm is greedy but provably converges to a unique history similar to Nakamoto consensus, except it can do so even when many blocks are in progress. The formal guarantee is that as blocks accumulate, the probability of a given block's ordering changing (i.e., a fork reversal) decreases exponentially, just as with Bitcoin confirmations - but this assurance is achieved at much higher block rates. In practical terms, Kaspa transactions are deeply buried under many blocks much faster than on Bitcoin, making them very secure against reorganizations in seconds. The Kaspa team notes that GhostDAG's ordering "becomes exponentially harder to reverse as time goes on," even at high block creation rates. Finality is fast; the network achieves what could be called a thermodynamic irreversibility of transactions at a human scale.
Given that all blocks are preserved, Kaspa miners have no incentive to withhold or strategically selfishly mine to orphan others' blocks - behavior that can be rational in faster blockchain contexts. Kaspa's strategy of maximum information revelation (each block references all tips it knows) means that the network is quickly informed of all parallel blocks. This floods the graph with knowledge, reducing uncertainty. In information theory terms, Kaspa minimizes the entropy of the network state by ensuring that no invisible forks persist for long; everything is integrated. The "maximum revelation principle" essentially aims to reduce system entropy (uncertainty) by sharing data quickly. This again aligns with physical principles: to maintain order, you want to propagate information (or energetic signals) as efficiently as possible through the system.
It is important to note that Kaspa achieves this without compromising security or decentralization. It still uses proof-of-work, meaning that the validity of each block is guaranteed by the real energy expended. And because blocks are smaller and frequent, node bandwidth and storage have been carefully managed (with techniques like pruning and efficient UTXO management) so that even a home computer can keep up. The result is a network that offers "proof-of-work grade security and decentralization with performance comparable to leading proof-of-stake networks." Unlike some projects that have solved the scalability problem by abandoning PoW or centralizing block production, Kaspa preserves the physical security of Nakamoto consensus's proof-of-work. There is no reliance on privileged validators or committee checkpoints - it's still miners competing with hashes - but now, each miner's block finds its place in history, and network throughput is no longer throttled by the slowest participant.
To put it simply, Kaspa's GhostDAG protocol removes the structural bottleneck that Bitcoin had deemed inevitable. The old "security vs. speed vs. decentralization" trilemma is, according to Kaspa, entirely solved in practice. By departing from the linear chain model, Kaspa opens the floodgates of throughput without sacrificing Nakamoto security - a feat many researchers thought impossible for years. All this leads to a system where blocks arrive continuously like droplets in a well-synchronized fountain, rather than the punctual, intermittent blocks of Bitcoin's clock. Transactions on Kaspa are confirmed in seconds and finalized (with negligible reorganization probability) typically in a few tens of seconds. In fact, Kaspa's design goal was confirmation times limited only by network latency - as fast as information can physically travel over the Internet. The network already delivers fully confirmed transactions in about 10 seconds on average, and this number decreases as block rates increase. From a user's perspective, this means that sending value via Kaspa feels almost like a credit card payment or a cash transfer - settlement is almost instantaneous, but with the added benefit that it is irreversible and trustless.
Achieving Throughput at the Speed of Light
One way to appreciate Kaspa's alignment with physical principles is to examine its handling of latency, the delay from one side of the world to the other. The global Internet round-trip time (RTT) - essentially the time it takes for a signal to go to the antipodes and back - is on the order of 200 milliseconds (0.2 seconds) in the best case (limited by the speed of light in fiber and network hops). Traditional blockchains like Bitcoin operate orders of magnitude slower than this limit (600 seconds per block), so network latency is not a major factor in their design; they live in a comfortable, slow equilibrium regime. But Kaspa has boldly ventured into the regime where block times are on the order of network latency - currently 100 milliseconds per block in the new upgrade (10 BPS), which is actually faster than one-way propagation to the other side of the Earth. This is a critical threshold. Moving from a 1-second block time to a 0.1-second block time is not just a 10-fold quantitative improvement; it's a qualitative leap that required rethinking consensus.
Why? If you try to run a single-chain (linear) consensus with 100ms blocks in a global network, you would have total chaos - hardly has one node heard of a block than five others have already been found. Propagation delay would mean the network is never synchronized; forks would proliferate and consensus would break down or centralize (only the fastest connections would always win). Kaspa is the first proof-of-work system to demonstrate consensus in this sub-RTT regime, and it can do so precisely because its multi-leader GhostDAG can handle many simultaneous blocks elegantly. As lead developer Michael Sutton noted during Kaspa's Crescendo upgrade (which moved the mainnet from 1 BPS to 10 BPS), "Increasing the block rate to 10 per second, achieved by reducing block time to 100ms (< 200ms ≊ global RTT), can only be secured with a consensus protocol that inherently allows parallelism... Crossing the RTT threshold is therefore a qualitative, not just quantitative, leap." In other words, Kaspa's design is fundamentally aligned with the physical limits of information transfer - it is structured to operate at the maximum speed that the laws of physics (speed of light, network bandwidth) allow, whereas a linear chain cannot safely cross this limit without sacrificing security or assuming a smaller network radius.
It is worth emphasizing how remarkable this is in the context of distributed systems. Kaspa achieves global, asynchronous consensus with block times shorter than global communication delays. And it does so without shrinking the network or requiring special trust setup. The network remains vast and permissionless - nodes can be anywhere in the world, connected by standard Internet links - and yet Kaspa produces and confirms blocks faster than any single chain could imagine under these conditions. The GhostDAG protocol essentially enables what classical consensus theory would have believed impossible under a strict longest-chain rule: keeping everyone in agreement despite constant mini-forks (parallel blocks). The idea is that by allowing these forks to exist and then probabilistically ordering them, you embrace chaos and organize it, rather than trying to prevent it entirely. The result is maximum throughput.
Upon activation of the Crescendo hard fork, Kaspa developers noted that the system was designed such that even at 10 BPS, a supercomputer was not needed to run a node. The Rust implementation and protocol optimizations ensure that an average PC with a home Internet connection can keep up with 10 blocks per second and thousands of transactions per second. This demonstrates a design ethic focused on efficiency at all levels - not just raw throughput, but also efficient use of computing resources and bandwidth. For example, blocks remain compact, and the DAG structure is pruned and managed so that it does not become unwieldy. Kaspa even includes new techniques (like the upcoming DAGKnight and pruning strategies) to adapt to network conditions and limit state size. All these choices reflect an almost physical minimalism: eliminating waste, whether it's wasted hashing power, wasted time, or wasted storage. If Bitcoin mining is sometimes criticized for producing a lot of heat (wasted energy per transaction), Kaspa significantly reduces energy per transaction by increasing throughput and using a more energy-efficient hashing algorithm (kHeavyHash). The Kaspa team explicitly designed kHeavyHash to be compatible with optical and light-resource mining, meaning it could potentially run on specialized hardware that uses much less electricity. Combined with the DAG's "no wasted blocks" policy, this makes Kaspa less energy-intensive than other PoW networks per transaction or per value transferred. Simply put, Kaspa can do more with each joule of energy miners put into it - a testament to its superior engineering. Even independent observers note this efficiency: "The KHeavyHash algorithm is designed to optimize energy consumption, making [Kaspa] less resource-intensive compared to... Bitcoin." We can see this as an improvement in the system's thermodynamic efficiency: a greater portion of the input energy is converted into secure, finalized transactions (useful work) rather than wasted hashing or waiting time.
By pushing physical limits responsibly, Kaspa positions itself as a highly thermodynamically efficient monetary network. It aligns block production cadence with the fastest possible communication, eliminates redundant work, and ensures that every bit of work contributes to transaction ordering. By analogy, if Bitcoin is like an old heat engine that produces a lot of wasted heat and runs at low speed, Kaspa is like a modern turbine operating near its theoretical efficiency limit - extracting the most useful motion (transaction throughput) possible from each unit of fuel (hashing energy). The laws of physics set a strict ceiling, and Kaspa is determined to reach that ceiling. This alignment with the "directional flows" of technological evolution (more output for fewer inputs) suggests that Kaspa follows an evolutionary trajectory we have observed in many other systems - from single-core to multi-core processors and parallel processing, from dial-up to broadband Internet, from horse-drawn carriages to multi-lane highways. Systems that leverage parallelism and reduce internal resistance inevitably outperform those that remain stuck in a single sequential process.
Less Friction, Better Value Retention
The technical virtues of Kaspa's design have profound economic implications. When we reduce entropy and friction in a monetary system, we create a more hospitable environment for value to reside and circulate. Consider an economy as a living ecosystem or perhaps an electrical grid: if energy (or money) can flow freely where it is needed with minimal losses, the system thrives and grows. Kaspa's low-latency, high-throughput network means that value can be exchanged quickly and cheaply by anyone, anywhere, without being siphoned off by intermediaries or high waiting costs. This property naturally attracts usage - users will prefer a system where their payments are confirmed in a second over one where they wait an hour, especially when security is comparable. As usage increases, liquidity and capital gravitate towards the network, increasing its utility in a feedback loop. Economics 101 tells us that, given two options, people will choose the one with the lowest transaction costs (all else being equal), and money will flow through the channel that offers the least impedance to trade. Kaspa presents itself as this low-impedance channel: "minimum dissipated work, minimum transactional impedance, maximum monetary clarity," as one observer described the convergence point where capital will flow. With Kaspa, traditional barriers - confirmation delays, throughput caps, high fees during congestion - are significantly minimized, so the "pipe" for monetary energy is wide and smooth.
Plan K, in an interview on Kaspa's economics, used a biological analogy to describe how efficient money directs energy: good money is like a plant's vascular system that channels nutrients (energy) to the photosynthesizing leaves (productive work), rather than allowing resources to be sucked up by parasites or inactive parts. In this analogy, Kaspa can be seen as a form of low-entropy money that encourages efficient energy flow. Its speed and capacity ensure that economic energy (value) moves to productive uses (actual transfers of goods and services) instead of being wasted in backlogs or arbitrage between layers. Meanwhile, its proof-of-work basis prevents the energy diversion that occurs with "easy money." Fiat currencies, for example, have been compared to a parasitic vine in Plan K's analogy - they can be inflated or copied by central authorities, effectively siphoning energy from the productive economy by diluting value. Kaspa, like Bitcoin, immunizes itself against such dilution by requiring real work for the creation of new coins and strictly limiting supply growth. As Plan K noted, "Gold, Bitcoin, and Kaspa are similar to [hormones] that cannot be copied, preventing any energy diversion." In simpler terms, these hard moneys lock in the energy that was used to produce them; they offer a secure reservoir for economic value without leakage through debasement.
Kaspa extends this principle of hard money to the realm of daily usability. Bitcoin proved that a decentralized network can store value securely (low entropy over time), but Kaspa also aims to move value efficiently (low entropy in transactions). By marrying Bitcoin's unforgeable cost with a frictionless transactional layer, Kaspa positions itself as a complete solution for money: a store of value, a medium of exchange, and a unit of account all in one, without the usual compromises. It is instructive to recall why historically gold needed a substitute (like paper money or fiat currency) for daily transactions - because gold was heavy and slow to move, introducing friction. Bitcoin, being slow and with limited throughput, has similarly invited Layer 2 networks or competing coins to fill the gap for fast payments, essentially ceding the role of medium of exchange to "softer" currencies. Kaspa, on the other hand, is fast and scalable enough not to require a secondary monetary network to handle volume. It can be both the high-integrity settlement layer and the high-speed transaction layer. This suggests a future where economic activity will not need to constantly switch between a "store of value network" and a "payment network" (with all the exchange friction and security compromises that entails) - instead, a single network can do it all efficiently. Indeed, proponents argue that because Kaspa has solved the trilemma, "there is no longer a gap in the monetary market that Kaspa does not fill," eliminating the need for slower base stores like Bitcoin or faster but weaker alternatives. Whether Bitcoin remains a high-value settlement layer and Kaspa more for exchange, or Kaspa eventually absorbs both roles, the market will decide. But one thing is clear: systems that waste less and deliver more will win out over those that don't in the long run. This is natural selection applied to monetary systems.
Less friction also means that miners and users are better aligned in the Kaspa ecosystem. In Bitcoin, users sometimes complain about paying high fees during congestion (which ultimately go to miners), and miners deal with variance and losses due to orphans. In Kaspa, high throughput keeps fees low (because capacity is abundant), and the orphan-free design means miners don't lose rewards due to network latency. Miners still earn their fair reward - in fact, Kaspa's block reward is distributed over many more blocks per unit of time, which, paradoxically, makes the mining process more granular and fairer (multiple miners per second can earn rewards, rather than a single winner every 10 minutes). This can reduce mining variance and centralizing pressures (because in Bitcoin, a mining pool that finds a block slightly faster wins a 100% reward over 10 minutes, while in Kaspa, many miners each get a smaller reward every second - a "multi-leader" system where the advantage is averaged out). More miners can include blocks almost simultaneously, which could reduce the monopolistic tendency of one miner dominating a given time slice. The "increased competition within each latency round" even has implications for reducing MEV (miner extractable value) and manipulation - because when blocks are parallel, it is much harder for a single actor to control transaction ordering. Indeed, Kaspa's parallelism adds a bit of chaos that promotes fairness: it becomes impossible to apply certain exploits that require strict control over ordering, thus reducing the entropy of market outcomes (market prices and transactions reflect true supply and demand, not miner interference). This is another example of how Kaspa's approach tends to preserve value within the system - by making the system's behavior more thermodynamically irreversible, in the sense that no actor can easily rewind or reorder transactions for their profit, network state changes (executed transactions) are authentic and durable. It aligns economic flows with an almost physical inevitability: once something happens in Kaspa, it's essentially done and cannot be easily undone or cheated.
From a macro perspective, if one considers the global competition of currencies and networks as an evolutionary landscape, a system like Kaspa that offers low resistance and high integrity will tend to accumulate "monetary mass." Over time, liquidity begets liquidity - users go where other users and merchants are. If Kaspa continues to offer Bitcoin-like security with significantly better performance, it is reasonable to think that more economic activity will move onto Kaspa. We have already seen historically that fiat currencies replaced gold for transactions due to their lower friction, although gold is a superior store of value; and now cryptocurrencies challenge fiat currency by combining hardness with digital speed. Kaspa can be seen as the next step: combining the ultimate hardness of PoW money with the ultimate speed of modern networks. In the language of physics, Kaspa could be the "gravitational endpoint" for monetary energy - a massive attractor that draws capital because it represents a state of minimum potential energy (i.e., you cannot easily find a system where your money is safer and easier to use at the same time). When there is no easier path (lower energy state) for value to flow, you have reached equilibrium, and Kaspa aims to be that equilibrium point for decentralized money.
Irreversibility and the Arrow of Time in Kaspa vs. Bitcoin
A striking aspect of proof-of-work systems is how they establish an arrow of time. Each block is an irreversible event; once the work is done and the block accepted, undoing it would require expending an equivalent (or greater) amount of energy. This unidirectional function of work gives blockchains a temporal direction: just like entropy in physics, it is easy to go forward (mine new blocks, increase entropy) but extremely difficult to go backward (undo blocks, decrease entropy) without external intervention. Bitcoin's blockchain, secured by energy, is often compared to the arrow of time - a sequence of increasingly "established" history. Kaspa inherits this property but accelerates it. Because blocks arrive so quickly and GhostDAG rapidly deepens the ledger history, transaction irreversibility compounds faster in Kaspa than in Bitcoin. The probability of reversing a transaction in Kaspa decreases exponentially with each passing second, as multiple new blocks cement the order. In Bitcoin, six blocks (about an hour) are typically referenced for high confidence; in Kaspa, a similar level of security could be achieved in perhaps a dozen blocks, which at 1 block/sec was about 12 seconds (and at 10 blocks/sec, it's a little over a second, although other latency factors come into play).
This means that Kaspa's ledger finality approaches something very close to real-time irreversibility. The system's behavior reflects an irreversible thermodynamic process that very quickly reaches a point of no return. For example, if two conflicting transactions (double-spend attempts) are issued, Kaspa's rapid block inclusion and ordering will decide the winner and stack confirmations on it within seconds, making the loser's attempt to reverse increasingly futile. In Bitcoin, this period of uncertainty (entropy) could last many minutes and even then can be exploited by an attacker with enough hashing power in a low-entropy state (before many confirmations accumulate). Kaspa reduces this window, making the cost of reversing history extremely high almost immediately. We can view this as Kaspa increasing the thermodynamic gradient an attacker must climb - a steeper hill that gets steeper faster. This is again related to efficiency: the network does not waste time converting hashing power into security (order), so an attacker does not have the "luxury" of a long vulnerability window to exploit. The entropy of uncertainty is quickly expelled from the system, leaving a very ordered state (confirmed transactions) that is stable.
Another perspective is that of Landauer's principle, a concept in physics that states that erasing a bit of information has an irreducible energy cost (heat dissipation). In blockchains, "erasing" a transaction (via a reorganization that removes a confirmed transaction from history) is extremely energy-costly - which is why large reorganizations are infeasible if honest miners control the majority of hashing power. Kaspa ensures that transaction data bits are incorporated into many blocks (information bits) almost immediately, so the information takes root and becomes thermodynamically expensive to erase. Essentially, Kaspa aligns information theory with thermodynamics: information (the ledger state) acquires entropy-resistant permanence quickly, rooted by proof-of-work. And because Kaspa uses its input energy more efficiently (no wasted blocks, more confirmations per unit time), it arguably achieves higher "irreversibility per unit of energy" than Bitcoin. Every joule of mining in Kaspa contributes to the finality of many transactions, while in Bitcoin, every joule secures fewer transactions (and some joules are spent on blocks that might not even count).
The arrow of time metaphor is appropriate: Bitcoin's arrow moves slowly but inexorably forward, taking longer to firmly establish history, while Kaspa's arrow flies at high speed, quickly fixing events in time. Both arrows point in the same direction - imposed by the second law of thermodynamics (energy consumption) - but Kaspa's covers more distance (ledger depth) per unit of time. This not only has practical advantages (user experience, throughput), but it philosophically indicates that Kaspa's design is in harmony with the "natural" direction of complex systems: towards more order achieved in less time by expending energy. If Bitcoin showed that energy + time = security, Kaspa shows that with better design, you can achieve equivalent security with the same energy in much less time, simply by eliminating internal inefficiencies. It violates no fundamental laws; it just doesn't waste the opportunities that Bitcoin leaves on the table.
Conclusion: Kaspa as the Efficient Frontier of Monetary Networks
By examining Kaspa through the dual lenses of physics and economics, we see a theme emerging: systems evolve towards optimal efficiency in processing energy and information. In economics, money has evolved from cumbersome commodities to gold, to gold-backed paper, to digital networks - each step aiming to reduce friction while preserving trust and value. In computing and networking, we have moved from serial to parallel processing, from analog delays to near-light-speed signals. Kaspa represents the convergence of these evolutionary paths in the realm of decentralized money. It takes the hardness and finality of energy-backed proof-of-work - the aspect that makes Bitcoin a form of "digital gold" - and supercharges the efficiency of the system that uses this energy. The result is a network that can be described as a value engine: it converts electrical energy (hashing work) into digital economic value (secure transactions and coin issuance) with minimal waste, channeling that value quickly where it needs to go.
In positioning Kaspa against Bitcoin, it is not about rivalry but about progress in decentralized architecture. Bitcoin was the prototype that proved a thermodynamic approach to money worked. Kaspa is an evolution that refines the architecture to minimize waste (entropy) and maximize throughput (useful work) without losing the essence of what made Bitcoin great (decentralization and security via proof-of-work). We have only compared Kaspa to Bitcoin because both share the fundamental foundation of PoW and sound monetary policy, differing primarily in structural design. And that difference - a blockDAG vs a blockchain - has made all the difference. Kaspa's blockDAG is a natural solution to Bitcoin's bottlenecks, almost obvious in retrospect: if one lane is too slow, add more lanes; if discarding blocks wastes energy, find a way to keep them all; if waiting for global synchronization causes latency, allow some asynchrony and then resolve it algorithmically. These are, in a sense, common-sense optimizations once technology allowed them to be implemented. GhostDAG's brilliant insight was to find a way to make many leaders (miners) work together at once without chaos - like a well-orchestrated symphony rather than a solo performance. This shows that order can emerge from apparent chaos with the right rules, echoing how physical systems self-organize when constraints are wisely applied.
The end result of Kaspa's design choices is a system that, according to some, constitutes a natural culmination in efficient value computation. It is as fast as physics allows, as secure as proof-of-work can be, and as decentralized as a globally inclusive network should be. Could we go faster or be more efficient without breaking the fundamental link between money and thermodynamics? Probably not much - not without new physics or compromising trust. Kaspa already aims for 100 blocks per second in the future, approaching an almost continuous block stream, and its developers are integrating adaptive features (like DAGKnight) that adjust confirmation speed to conditions. We are approaching the practical limits of on-chain scaling in a decentralized context. Any significant further gains would likely require fundamentally different approaches (or acceptance of centralization). In this sense, Kaspa is the efficient frontier - you cannot get significantly higher throughput or lower latency at scale without incurring more waste or risk than Kaspa. It has found a balance that uses resources optimally.
For savvy crypto professionals and researchers, Kaspa offers a fascinating case study where the principles of thermodynamics, information theory, and economics converge. It validates the idea that a decentralized financial network can be analyzed in the same way as a physical system - with energy inputs, work outputs, and inefficiencies as entropy. By reducing these inefficiencies, Kaspa doesn't just perform better; it fundamentally creates a more sustainable and attractive economic system. A system with less waste means miners' work goes further, users' fees stay lower, and more value circulates rather than being burned in overhead. Over time, this attracts more participation, more investment, and strengthens network effects. It's analogous to how an efficient engine not only saves fuel but enables new capabilities - longer trips, heavier loads - so an efficient blockchain enables more economic activity and use cases that would stifle a slower chain.
In conclusion, Kaspa can be seen as the culmination of over a decade of research into scaling Nakamoto's invention without losing its soul. It shows that the laws of physics and sound economics are not enemies of decentralization, but guides for improving it. Kaspa's success would mean that the monetary system that most faithfully follows the path of least resistance and least entropy production will prevail - a result highly aligned with physics. In practical terms, Kaspa represents a high-throughput, low-friction, secure network that could carry the value of nations within a single protocol, accessible to all, and limited only by the speed of light and the honesty of the majority. If Bitcoin opened the door to a thermodynamic financial era, Kaspa accelerates into it, making the flow of economic energy as efficient as the flow of electrons. In the grand narrative of technology and money, Kaspa stands out as compelling proof that efficiency is destiny: given two systems, the one that best minimizes waste and maximizes useful work will attract the future. And Kaspa presents a persuasive and technically sound argument that it is that system - an evolutionary leap towards a frictionless, value-preserving, and ultimately more human-aligned monetary network.
Chapter 13: Kaspa vs Bitcoin Ordering
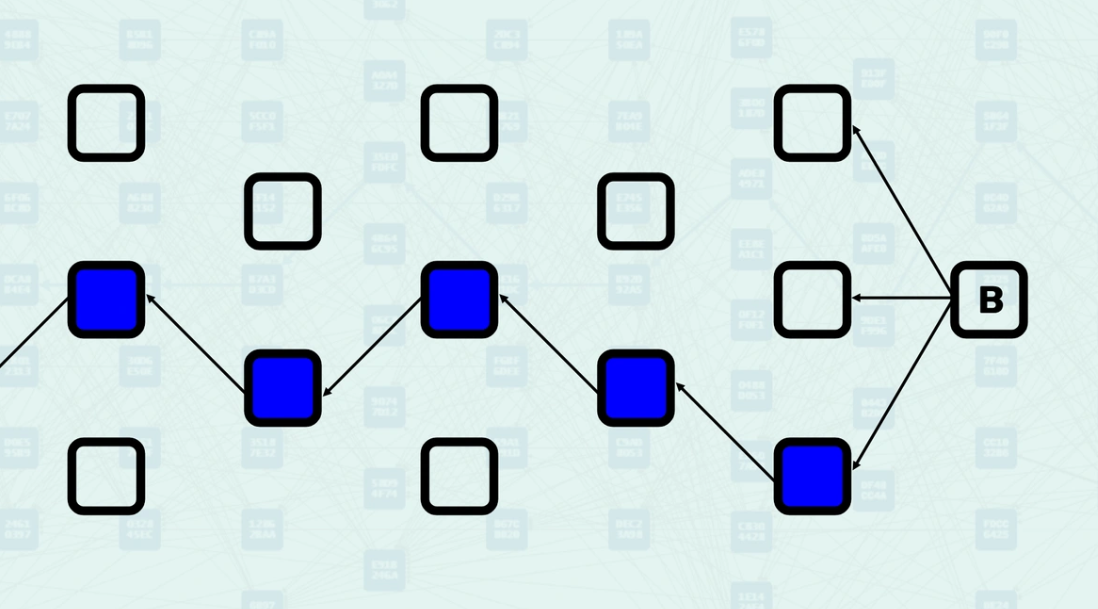
Block Selection and Ordering: Heaviest Chain vs Blue Work
Bitcoin's Heaviest Chain Rule - Sequential Selection
Bitcoin's consensus mechanism operates on a linear principle where the network maintains a single chain of blocks. When miners create new blocks simultaneously, the network faces a choice between competing chains. The heaviest chain rule resolves this by selecting the chain with the most accumulated proof-of-work, thus choosing the path that represents the greatest computational investment. This approach creates a winner-take-all scenario, where only one chain survives while all competing blocks become orphaned. Orphaned blocks, although containing valid transactions and representing real computational work, contribute nothing to network security or transaction processing capacity. This design ensures clear ordering but inherently limits throughput as only one block can be accepted at each height level. In this example, you can see how blocks are discarded by Bitcoin.
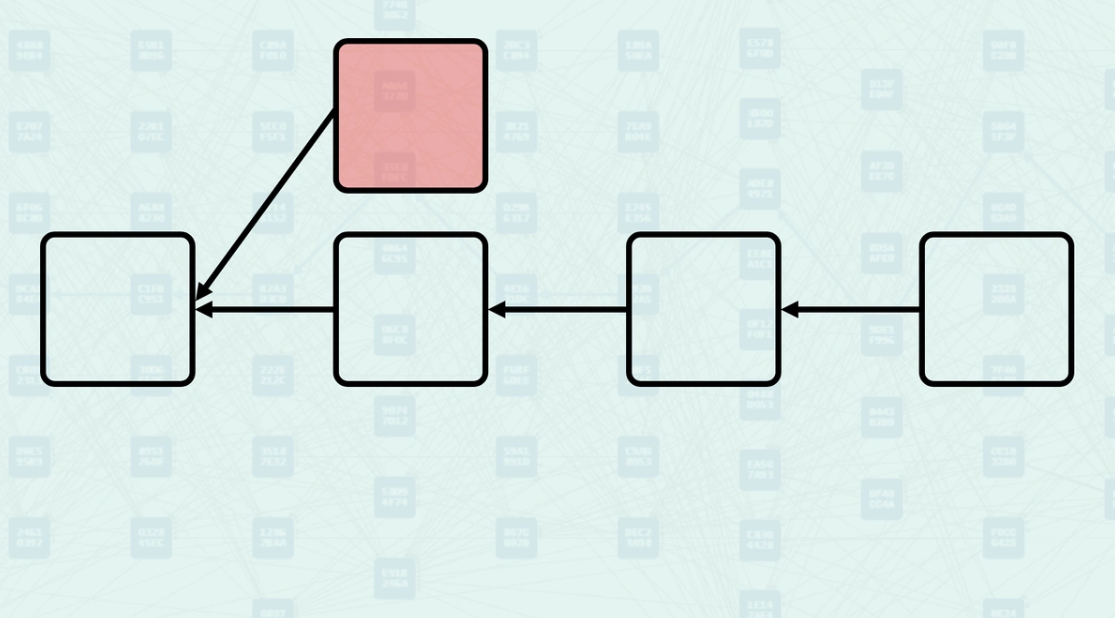
Kaspa's Blue Work Selection - Parallel Integration
Kaspa's GHOSTDAG protocol extends this approach by operating within a Directed Acyclic Graph (DAG) structure where multiple blocks can coexist and contribute to network security. Instead of discarding competing blocks, GHOSTDAG classifies them as "blue" (honest, contributing to consensus) or "red" (potentially conflicting but still retained). The "blue work" metric represents the accumulated proof-of-work only from blue blocks in the DAG. This selective accumulation ensures that only consensus-valid blocks contribute to the security calculation, while preserving the work and transactions of red blocks within the overall structure. In this example, you can see that the block that was discarded by Bitcoin is included in Kaspa's DAG, even when k = 0.
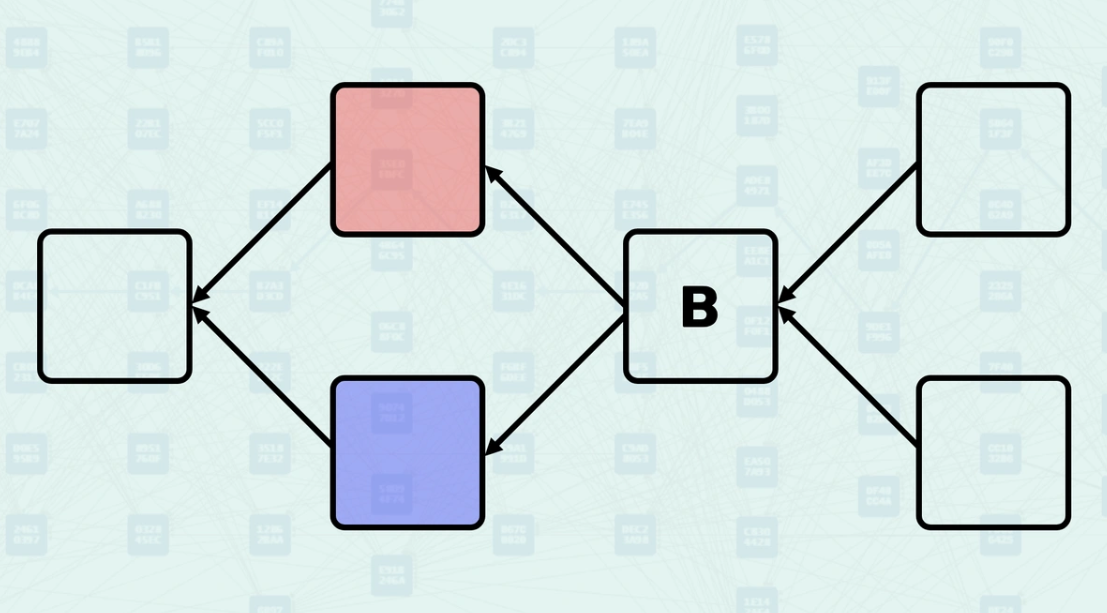
Parent Selection and Main Chain Formation
When a new block enters the DAG, GHOSTDAG must select a "Selected Parent" from several possible parent candidates. This selection process examines the "blue work" value of each potential parent and chooses the one with the highest accumulated "blue work" value from the honest blocks. Here is block B, selecting the best parent (the parent with the most work) among its parents.
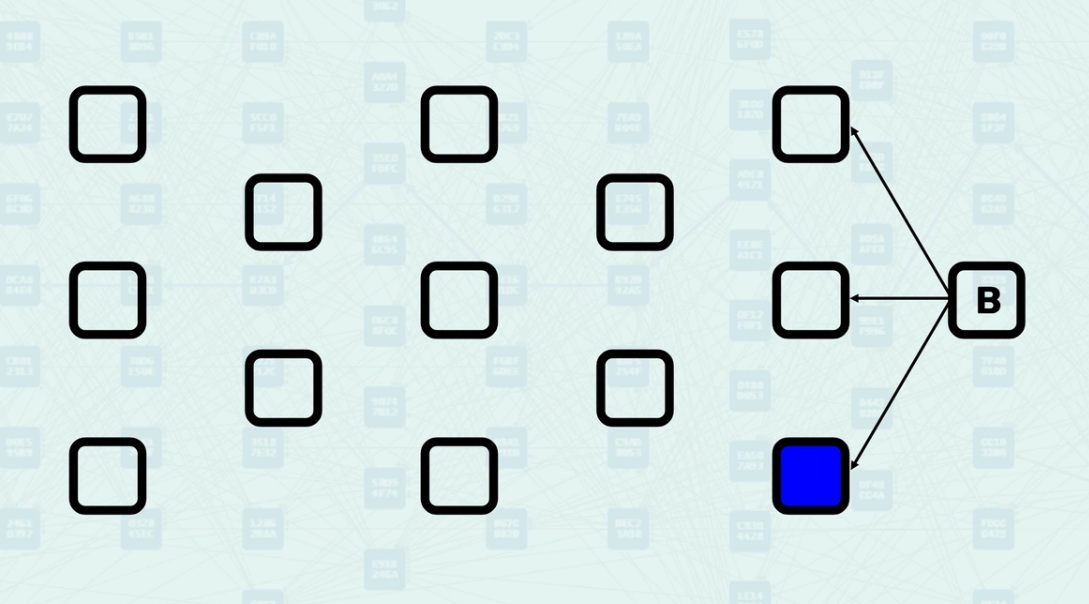
This selected parent becomes the basis for establishing a main chain within the DAG. The main chain provides a deterministic ordering mechanism similar to Bitcoin's linear chain, but operates in the more complex DAG environment. After selecting the main parent, the protocol processes all remaining blocks in what is called the "Mergeset" - blocks that are included in the DAG but were not chosen as the Selected Parent. After selecting a parent, we can follow the Selected Parents through the DAG; this creates a chain you can see in the image here.
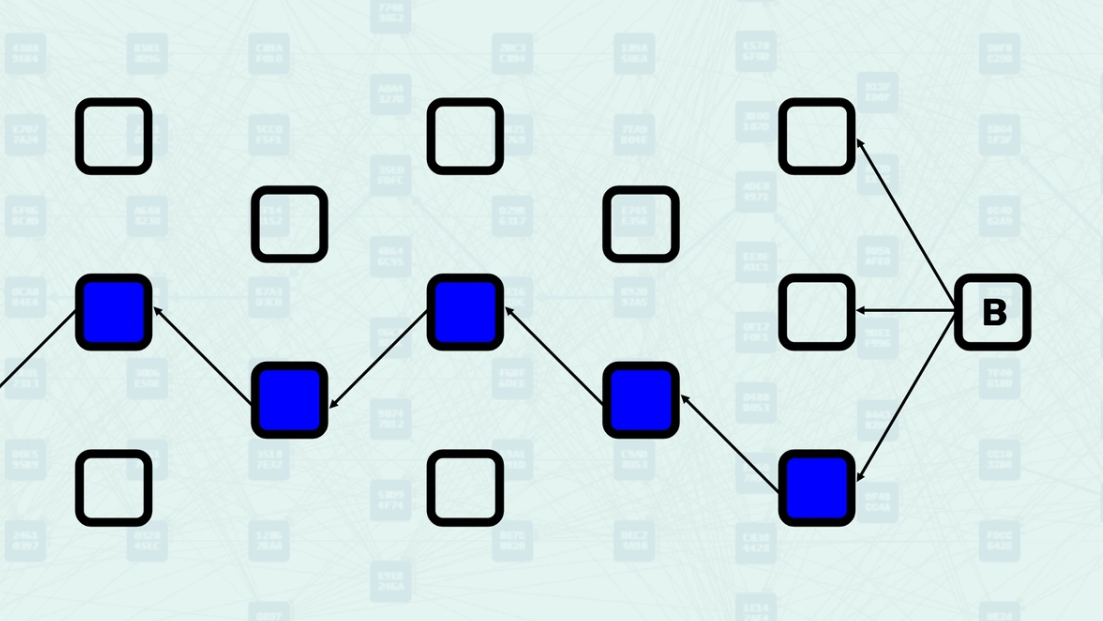
Ordering and Transaction Processing
The main chain created by "blue work" selection serves as the primary ordering mechanism for transaction processing. Transactions are processed first from the Selected Parent, then from the Mergeset blocks in a consensus-agreed order. This creates a deterministic sequence that all nodes can reproduce, ensuring consistent transaction ordering across the network.
Fundamental Architectural Differences
Bitcoin's Approach: Creates a single linear sequence where each block has exactly one parent. Conflicts result in the permanent exclusion of competing blocks, with only the winning chain contributing to network security.
Kaspa's Approach: Maintains a DAG structure where blocks can have multiple parents and children. Conflicts are resolved through classification rather than exclusion, allowing multiple blocks to contribute to network security while maintaining consensus via the main chain.
Implications for Throughput and Security
Bitcoin's linear approach offers strong security guarantees but limits throughput to about one block every 10 minutes. The orphaning of competing blocks represents a waste of computational resources and a loss of transaction capacity.
Kaspa's "blue work" system allows for much higher throughput while maintaining security properties. By preserving both blue and red blocks in the DAG, the system captures a larger portion of the network's computational work and transaction processing capacity. The main chain ensures deterministic ordering despite the increased complexity, allowing for parallel block creation without sacrificing consensus reliability.
Bitcoin's rollback in 2013: A lesson in finality
In March 2013, the Bitcoin network experienced a critical event that contradicted its fundamental principle that "the longest chain is the valid chain."
- A chain split: A miner using Bitcoin Core version 0.8 produced a block incompatible with older versions (0.7). This caused a chain split (fork).
- Social coordination trumped protocol: Although the 0.8 chain became longer, core developers and large mining pools socially coordinated to abandon this chain and revert to the shorter but compatible 0.7 chain.
- Finality was broken: 24 blocks from the 0.8 chain were orphaned. The transactions they contained, once considered valid, were erased from Bitcoin's canonical history.
This event proved that Bitcoin's consensus is not purely deterministic and may require human intervention. In Kaspa, such splits are impossible. All blocks, even if mined simultaneously, are included in the DAG, and GHOSTDAG selects an ordered history consistently and algorithmically. There is no need for rollbacks or social coordination; finality is deterministic.
Chapter 14: Kaspa's Vision for Layer 2: ZK Rollups and Bridging
The need for Layer 2 solutions
While Kaspa offers impressive scalability at its base layer (Layer 1), the future of complex decentralized applications (DeFi, gaming, etc.) relies on Layer 2 solutions. These allow complex computations to be executed off the main chain, while benefiting from its security. Kaspa focuses on "Based ZK-Rollups," where Layer 1 (Kaspa) serves as the sequencing, data availability, and settlement layer.
The challenge: Proof at inclusion time vs. Execution uncertainty
Parallelized L1s like Kaspa introduce "execution uncertainty": transactions are included in the DAG before their final global order is determined. This is an advantage for MEV resistance, as it prevents miners from predicting the exact sequence.
However, this creates a conflict with ZK-Rollups, which, ideally, would require "proof at inclusion time." To generate a ZK proof, the pre-state must be known and unambiguous. But in Kaspa, this state is undefined at inclusion time due to parallel processing.
Kaspa's solution is to opt for multi-leader consensus and its execution uncertainty. Therefore, ZK proofs must be deferred and submitted to the L1 only after transaction order has converged and a clear state is established. This introduces a new challenge: what if the required proof never arrives?
Timebound Proof Settlement
The proposed model is "timebound proof settlement."
- Transaction data is first published to the L1 (data availability).
- Final settlement of its effects on the L1 depends on the submission and verification of a ZK proof within a defined time window (T).
- If a party involved in an operation fails to provide its proof within this timeframe, the operation fails, with penalties to ensure accountability.
This model allows for fast optimistic confirmations on the user side, long before final settlement on the L1, as each rollup has a direct interest in submitting its proof to maintain its own "liveness."
KIP-15 and Accepted Transaction Archive Nodes (ATANs)
A fundamental problem for L2s on Kaspa is pruning. How can an L2 refer to transaction data that has been pruned from the L1? ZK proofs are the long-term solution, but an interim solution is needed.
This is the purpose of KIP-15: to introduce Accepted Transaction Archive Nodes (ATANs). An ATAN sits between a pruned full node and a full archive node.
- It does not store full transaction data.
- It stores the headers of the selected chain and the hashes of all transactions.
A transaction hash is only 32 bytes, which represents a massive compression compared to the transaction itself. An ATAN can store years of transaction hash history with reasonable storage requirements (estimated at about 3-5 TB per year at full capacity). This allows an L2 to prove the existence and order of any past transaction without needing a full archive node, thus solving the data availability problem in a pruned environment.
Canonical L1<>L2 Bridge Design
To allow funds (KAS) to flow between L1 and L2, a "canonical bridge" is needed.
- Inbound (L1 to L2): A user sends KAS to a static delegation address on the L1. This operation is immediately validated by the L1, and funds are usable almost instantly on the L2.
- Outbound (L2 to L1): An outbound transaction requires internal authorization on the L2. Its validity must be confirmed on the L1 by submitting a ZK proof.
To do this, Kaspa uses "delegation" scripts. Instead of sending funds to the rollup's state address (which is dynamic), users send to static addresses that delegate their spending authorization to the ZK proof provided by the rollup. This simplifies the user experience and bridge fund management.
Chapter 15: The Igra Network: A Case Study of Kaspa's EVM-Compatible ZK Rollup
Igra Overview
Igra Network is an excellent practical example of Kaspa's vision for Layer 2. It is an EVM-compatible ZK rollup that uniquely uses Kaspa's BlockDAG as a decentralized sequencer and settlement layer.
This architecture aims to combine Bitcoin-like security with the speed and versatility of modern programmable chains, solving critical limitations of current Layer 2 solutions.
Key Components
- Base Layer (Kaspa): Serves as the decentralized sequencer. Igra's transaction order is fixed on Kaspa's BlockDAG by its mining nodes.
- Igra Node: Maintains the full state of the L2 and executes EVM transactions. It extracts sequenced transactions from the L1 and executes them.
- Igra Relay / RPC: Provides the bridge between users and the network. It exposes standard Ethereum RPC interfaces, allowing users to interact with Igra using wallets like MetaMask.
Bridging Mechanism and Deployment
Igra uses a multi-phase bridging approach for its native token, $iKAS, which is a wrapped version of KAS.
- Phase 1 (Community Bridge): Initially, bridging relies on a multisig (m-of-n) wallet controlled by signers chosen by the community. This is a trust model similar to that used for many cryptocurrencies' community funds. To withdraw funds, signers are required to process requests, with safeguards to ensure a transition to a trustless system.
- Phase 2 (MPC/ZK Bridge): In the future, this bridge will be replaced by a trustless solution.
- MPC (Multi-Party Computation) Bridge: Uses cryptographic techniques like FROST to allow a set of validators to sign transactions without any of them holding the full secret key. This enables permissionless bridging.
- ZK Bridge: The ultimate solution. A user can submit a ZK proof to the L1 proving that they burned $iKAS on the L2. A script on the L1 will verify this proof and unlock the corresponding amount of KAS.
The Caravel Testnet
Igra's deployment is done in stages, starting with the "Caravel" testnet. This launch takes place in several phases:
- Activation: The network is activated on Kaspa's testnet.
- Community Testers: Node software is distributed to a limited group of testers to gradually increase network activity.
- Public Access: The software is made public, allowing anyone to run a node and participate.
This careful deployment process is essential, as Caravel brings the full Ethereum protocol to Kaspa's consensus, which operates at speeds yet unexplored in the EVM world. Intensive testing and several iterations are necessary to ensure stability and performance.
Chapter 16: Transaction Throughput and Collisions in Kaspa's BlockDAG
The Challenge of Transaction Collisions
What makes DAGs incredibly fast is the ability to parallelize: since blocks created in parallel are all considered valid, increasing the rate of parallel blocks does not harm security. However, a question arises: if we create 10 blocks per second, is our transaction throughput really 10 times higher?
Not quite. The nuance is that parallel blocks can contain the same transaction, and it's not fair to count the same transaction multiple times. We should be interested in effective TPS, i.e., the number of unique transactions included on average.
Random Selection Analysis
Assuming miners choose transactions to include randomly (which is a reasonable approximation, as we will see), we can analyze the effective TPS.
Mathematical analysis shows that even in the worst case (where block capacity exactly matches the number of available transactions in the mempool), the network includes at least (1 - 1/e) ≈ 62.3% unique transactions. This is a floor; in practice, when the mempool is larger than block capacity, efficiency tends towards 100%.
The result is that effective TPS increases almost linearly with the block rate. A 10x increase in block rate translates to an 8-9x increase in effective TPS, which is a significant improvement.
What about Dishonest Miners?
One might worry that "greedy" miners would try to manipulate transaction selection to maximize their profits, for example by all choosing the same high-fee transactions, which would increase collisions and reduce effective TPS.
Game theory shows us that this is not an optimal strategy. Random selection is a "weak equilibrium." This means that if a single miner deviates from this strategy, they can gain a slight advantage. However, if many miners deviate and all choose the same high-fee transactions, they end up competing directly for the same fees, and their expected profit decreases. In the end, the most rational strategy for a miner (who cannot predict what others will do) is to diversify their choices, which approximates random selection.
Potential Solutions for High Collisions
If, in practice, a high collision rate were observed, several solutions could be implemented:
- Transaction Bucketing: Blocks could be required to only include transactions whose hash matches certain digits of the block's own hash. This would divide transactions into "buckets," and blocks would only compete for transactions in the same bucket.
- Monopolistic Auction Mechanism: A mechanism where miners can include any transactions they want, but the fees for all transactions in the block are set at the level of the lowest fee among the included transactions. This incentivizes miners to include more transactions (to increase volume) rather than focusing only on those that pay the most, which naturally encourages diversification.
In conclusion, although transaction collisions are a consideration in BlockDAGs, Kaspa's architecture and game theory dynamics ensure that effective throughput remains high and scales robustly with the block rate.
Chapter 17: Kaspa's Fee Market: A Game Theoretical Perspective
The Importance of the Fee Market
A cryptocurrency's fee market is extremely important for its long-term security. Once block rewards become negligible, transaction fees remain the primary subsidy for network security. It is therefore crucial to understand the dynamics of the fee market that a protocol induces.
The Three Evils of Bitcoin's Fee Market
Bitcoin's fee market, due to its "single leader per round" consensus, exhibits properties that can be described as "three evils":
- Race-to-the-bottom: When the network is not congested, demand is lower than the supply of block space. Users have no incentive to pay high fees, as their transactions will be included anyway. Fees tend towards the minimum, which can make mining unprofitable and threaten network security.
- Price aberration: When the network is congested, a very small increase in fees can make a transaction go from "never included" to "included in the next block." The price does not reflect a gradual service.
- Starvation: In a congested network, low-fee transactions can be perpetually excluded, as they can never outbid high-fee transactions. This creates a barrier to entry and raises questions about the egalitarian ethos of the blockchain.
These dynamics are a direct consequence of a single miner winning the entire pot each round.
How Kaspa's Multi-Leader BlockDAG Improves the Fee Market
In Kaspa, multiple miners create blocks in parallel each round (multi-leaders). If multiple miners include the same transaction, they share the reward probabilistically. This radically changes the game dynamics for miners and users.
- Against the race-to-the-bottom: Because miners are in competition, it becomes rational for them to include transactions even if the network is only partially utilized, in order to diversify their revenue streams and avoid direct competition. Analysis shows that the fee market activates as soon as the network reaches 1/k of its capacity (where k is the number of leaders per round), instead of 100% for Bitcoin. With 10 leaders per round, the market activates as soon as 10% of capacity is used.
- Against starvation and aberration: Miners have an incentive to include a mix of transactions, including lower-fee ones. It is not always optimal to fight for the few highest-paying transactions, as the probability of winning those fees is reduced by competition. This creates a much smoother service curve: a slight increase in fees leads to a slight increase in the probability of inclusion, rather than a sudden change. Low-fee transactions still have a chance (even if small) of being included, which prevents starvation. A low probability of inclusion in a round translates to a reasonable average waiting time, rather than an infinite wait.
In conclusion, Kaspa's multi-leader architecture, a direct consequence of its high-frequency BlockDAG, creates an inherently healthier, more stable, and fairer fee market. By smoothing out the extreme "all-or-nothing" dynamics of single-leader blockchains, Kaspa builds a more robust economic foundation for its long-term security.
Conclusion
At the end of this journey through Kaspa's architecture and philosophy, one conclusion stands out: we are witnessing a true evolution in the field of distributed ledger technologies. Kaspa is not simply another cryptocurrency; it is a fundamental redesign of the principles established by Bitcoin, engineered for the high-speed digital age.
We have seen how its BlockDAG, governed by the GHOSTDAG consensus protocol, dismantles the linear chain bottleneck. By allowing the parallel creation and integration of blocks, Kaspa eliminates the waste of orphaned blocks, maximizes the energy efficiency of proof-of-work, and achieves transaction and confirmation speeds previously thought impossible for a decentralized PoW system.
We have explored its ingenious solutions to storage, with a multi-level pruning system that ensures long-term decentralization by maintaining low hardware requirements for nodes. We have also delved into its vision for the future, with Layer 2 solutions like ZK-Rollups, which promise to bring complex programmability and interoperability without sacrificing the security of the base layer.
Kaspa shows us that the blockchain trilemma -- the idea that one must choose between security, scalability, and decentralization -- may not be an immutable law, but rather a limitation of first-generation architectures. By drawing inspiration from the principles of physics and economics, Kaspa has designed a system that tends towards maximum efficiency, minimal friction, and optimal value retention.
The future of Kaspa is promising. With upgrades like DAGKnight that will formalize finality and ongoing research into MEV resistance and oracles, the project continues to push the boundaries of what is possible. Whether Kaspa becomes the backbone of the next generation of decentralized applications or coexists with other systems, one thing is certain: it has already left an indelible mark on cryptocurrency history by proving that a monetary system can be both as solid as gold and as fast as light.
We hope this book has provided you with the keys to understanding the depth and elegance of Kaspa. The journey is just beginning, and the best way to continue it is to get involved, ask questions, and keep learning.
Appendix A: Additional Resources
For those who wish to deepen their understanding of Kaspa, here is a list of essential resources, ranging from introductory articles to fundamental research papers.
Getting Started Articles
- Kaspa 101: An excellent starting point for understanding how GHOSTDAG works. Read here
- Scaling Bitcoin with BlockDAG: Explains why BlockDAG is a viable solution to Bitcoin's limitations. Read here
- Kaspa Pruning Primer: An introduction to Kaspa's pruning mechanism. Read here
- Kaspa GhostDAG 101 (Video): A comprehensive video overview of the technical concepts. Watch here
Research Papers (Deep Dive)
- PHANTOM and GHOSTDAG: The academic paper that laid the groundwork for Kaspa's consensus. Read PDF
- The DAGKnight Protocol: Kaspa's next-generation consensus protocol, designed for fast finality and attack resistance. Read PDF
- Prunality: The paper detailing the theory behind Kaspa's pruning mechanism. Read PDF
- Bitcoin Whitepaper: Satoshi Nakamoto's original paper, for historical context. Read PDF
Code and Development
- Rusty-Kaspa (Main Repository): The source code for the Kaspa node, written in Rust. View on GitHub
- Kaspa Improvement Proposals (KIPs): The repository containing all Kaspa Improvement Proposals. View on GitHub
Community and Discussion
- Discord: The main place for technical and community discussions. Recommended channels:
#research-general,#development. Join Discord - Telegram (R&D): A group where developers and researchers collaborate. Join on Telegram
- Research Forum: For in-depth discussions on KIPs and new technical concepts. Visit forum
Appendix B: Mathematical Analysis of Transaction Collisions (Simplified)
This chapter explores the issue of effective TPS (transactions per second) in a BlockDAG. When multiple blocks are created in parallel, they can contain the same transactions, which reduces unique throughput. Analysis shows that even with random transaction selection by miners, effective throughput remains high.
The key idea is that the probability of two miners choosing the same transaction decreases as the pending transaction pool (mempool) increases. Mathematical analysis (using probability theory and Taylor series) shows that even in a scenario where block capacity exactly matches the number of available transactions, the network includes at least (1 - 1/e) ≈ 62.3% unique transactions. This figure represents a minimum; in practice, efficiency is often much higher.
Furthermore, game theory suggests that miners have no significant incentive to deviate from this quasi-random selection. If all miners try to choose the highest-paying transactions, they end up competing for the same fees, which decreases their expected profit. A diversification strategy (random selection) is therefore a stable equilibrium (a "weak equilibrium").
In summary, Kaspa's parallelism does not significantly harm effective throughput, which increases almost linearly with the block rate.
Appendix C: Mathematical Analysis of the Fee Market (Simplified)
This chapter analyzes the dynamics of the fee market using game theory, comparing Bitcoin's "single leader" model to Kaspa's "multi-leader" model.
The Three Evils of Bitcoin's Fee Market:
- Race-to-the-bottom: When the network is not congested, users have no incentive to pay high fees, as their transactions will be included anyway. Fees tend towards the minimum, which threatens the long-term security of the network.
- Price aberration: When the network is congested, a very small increase in fees can make a transaction go from "never included" to "included in the next block." The price does not reflect a gradual service.
- Starvation: In a congested network, low-fee transactions can be perpetually excluded, creating a barrier to entry for less fortunate users.
How Kaspa's BlockDAG solves these problems:
In Kaspa, multiple miners create blocks in parallel (multi-leaders). If multiple miners include the same transaction, they share the reward (probabilistically). This radically changes the dynamic:
- Against the race-to-the-bottom: Because miners are in competition, it becomes rational to include transactions even if the network is only partially utilized. Analysis shows that the fee market activates as soon as the network reaches 1/k of its capacity (where k is the number of leaders per round), instead of 100% for Bitcoin. With 10 leaders per round, the market activates as soon as 10% of capacity is used.
- Against starvation and aberration: Miners have an incentive to include a mix of transactions, including lower-fee ones. It is not always optimal to fight for the few highest-paying transactions, as the probability of winning those fees is reduced by competition. This creates a smoother service curve: a slight increase in fees leads to a slight increase in the probability of inclusion, rather than a sudden change. Low-fee transactions still have a chance of being included, which prevents starvation.
In conclusion, Kaspa's multi-leader architecture creates a healthier, more stable, and fairer fee market, which is essential for the long-term security and viability of the protocol.